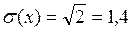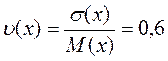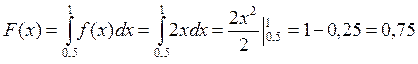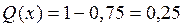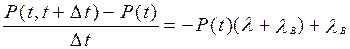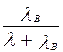Определить вероятность того что прибор проработает не более года

Экспоненциально распределенная случайная величина

На странице Непрерывная случайная величина мы разобрали примеры решений для произвольно заданных законов распределения (многочлены, логарифмы и т.п.). Здесь же мы разберем примеры только для одного типа СВ — распределенных по показательному (или экспоненциальному) закону.

Плотность распределения величины $X$ с экспоненциальным законом распределения задается формулой:

Функция распределения величины $X$:

Здесь $\lambda$ — единственный параметр данного распределения, полностью определяющий его свойства. В частности, числовые характеристики выражаются через этот параметр: $M(X)=1/\lambda$, $D(X)=1/\lambda^2$.

Экспоненциальное распределение моделирует время между двумя последовательными свершениями события, а параметр $\lambda$ описываетс среднее число наступлений события в единицу времени. Обычно с помощью этого закона описывают: продолжительность обслуживания покупателя, время жизни оборудования до отказа, промежуток времени между поломками и т.п.

В этом разделе мы приведем разные примеры задач с полным решением, где используются показательно распределенные случайные величины.

Примеры решений

Задача 1. Среднее время безотказной работы прибора равно 80 часов. Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти:
а) выражение его плотности вероятности и функции распределения;
б) вероятность того, что в течение 100 часов прибор не выйдет из строя.

Задача 2. Известно, что время работы прибора до первого отказа подчиняется показательному распределению со средним значением 1 год. Какова вероятность, что до первого отказа пройдет не менее 2 лет?

Задача 3. Установлено, что время ремонта телевизоров есть случайная величина $X$, распределенная по показательному закону с параметром $\lambda=1/3$ (1/день). Определить вероятность того, что на ремонт телевизора потребуется не менее 5 дней.

Задача 4. Время в годах безотказной работы прибора подчинено показательному закону, т.е. плотность распределения этой случайной величины такова: $f(t)=2e^<-2t>$ при $t\ge 0$ и $f(t)=0$ при $t\lt 0$.
1) Найти формулу функции распределения этой случайной величины.
2) Определить вероятность того, что прибор проработает не более года.
3) Определить вероятность того, что прибор безотказно проработает 3 года.
4) Определить среднее ожидаемое время безотказной работы прибора.

Задача 5. Предполагая, что случайное время обслуживания абонента службой «09» распределено по показательному закону и средняя продолжительность обслуживания составляет 1,5 минуты, найдите вероятность того, что абонент будет обслужен более, чем за 2 минуты.

Задача 6. Длительность телефонного разговора подчиняется показательному закону. Найти среднюю длительность разговора, если вероятность того, что разговор продлится более 5 минут, равна 0,4.

Задача 7. Случайная величина задана плотностью распределения $p(x)=ce^<-3x>$ при $x \gt 0$, и ноль в остальных случаях. Найти постоянную $c$, математическое ожидание, дисперсию и среднее квадратическое отклонение.

Задача 8. Непрерывная случайная величина $\xi$ распределена по показательному закону с параметром $\lambda$, равному номеру варианта 9. Найти плотность распределения случайной величины $\xi$, функцию распределения, построить графики этих функций. Найти математическое ожидание, дисперсию, среднее квадратическое отклонение случайной величины $\xi$ и вероятность того, что $\xi$ принимает значения, меньшие своего математического ожидания.

Задача 9. Случайная величина $\xi$ распределена по показательному закону с параметром 2. Найти $M_<\xi>$, $D_<\xi>$ вероятность попадания $\xi$ в интервал $(-1;2)$. Нарисовать графики плотности распределения и функции распределения $\xi$.

Задача 10. Известно, что $Х$ распределено по экспоненциальному закону $Exp(\lambda)$. Найдите вероятность события $|Х — МХ | \lt 3\sigma$ («правило $3\sigma$» для показательного распределения).

Решебник по теории вероятности онлайн

Больше 11000 решенных и оформленных задач по теории вероятности:

Источник

1.2.6. Расчет вероятности безотказной работы прибора

Рассмотрим примеры, в которых требуется вычислить вероятностьь безотказной работы и вероятность отказа работы прибора, в состав которого входят несколько элементов и используются различные способы их соединения между собой.

Пример 1.14. Прибор состоит из двух независимо работающих элементов. Вероятность отказа первого элемента равна P1= 0,1, а второго – P2 = 0,2.

1) Вычислим вероятность события A, если элементы соединены Последовательно,

Решение: Обозначим через A1 Событие, которое заключается в том, что откажет элемент А1 = <откажет первый элемент>, и через A2 —

Тогда данный прибор не будет работать (событие А), если выйдет из строя Хотя бы Один из элементов (или первый, или второй, или оба не будут работать). Такое состояние прибора можно описать, используя Определение суммы событий, т. е. A=A1+A2 . Из теоремы о вероятности суммы двух независимых событий [ формула (***)] получаем

Итак, вероятность того, что данный прибор Откажет Р (А) = 0,28.

Состояние прибора, когда он работает правильно, есть событие А — противоположное событию А, когда прибор откажет.

Тогда, используя свойства вероятности, можно найти Вероятность правильной работы А Данного прибора по формуле:

р ( ) = 1 – р (А) = 1 – 0,28 = 0,72.

2) Вычислим вероятность отказа прибора (событие А ), если элементы соединены параллельно:

Решение. Данный прибор откажет в том случае, если Откажут оба элемента Одновременно. Следовательно, отказ прибора в этом случае может быть представлен как Произведение Событий А1 и А2 , т. е. A=A1A2 . Так как элементы перестают работать Независимо друг от друга, то из независимости событий A1 и A2 получаем P(A) = P(A1) P(A2) = P1 P2 = 0,1 * 0,2 = 0,02.

Определение. События A1 A2 ¼ AN называют Взаимно независимыми, если для любой их части выполняется равенство

P() = p() p()¼P(), (1.5)

Источник

Разбор задания на вероятность про срок службы прибора (ЕГЭ и ОГЭ)

Среди заданий на теорию вероятностей, которые встречаются на ОГЭ и ЕГЭ по математике, есть такое, где нужно посчитать вероятность срока службы какого-либо технического прибора. И сегодня я предлагаю разобрать именно такой тип задач.

Вероятность того, что новый электрический чайник прослужит больше года, равна 0,93. Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.

На всем известном сайте, где разбираются задания по ЕГЭ и ОГЭ дано достаточно сложное решение, которое большинство учеников потом с трудом пытаются повторить.

Я же хочу предложить вам более удобное и понятное визуальное решение данной задачи. Чтобы всегда решать такие задания, нужно представить время как координатную прямую, где отметками являются года. нарисуем её.

Теперь добавим к данной прямой интервалы с вероятностью. В тексте задачи сказано, что чайник прослужит больше года с вероятностью 0,93.

С другой стороны вероятность того, что он прослужит больше двух лет, равна 0,87. Отметим и это тоже.

Нас же просят найти вероятность того, что чайник прослужит больше 1 года, но меньше 2-ух, этот интервал находится прям между нашими двумя отметками.

Когда мы визуально отмечаем интервал между 1 и 2, сразу напрашивается решение через вычитание из большего интервала величину меньшего.

Так и получается ответ: 0,06.

Рекомендую попробовать такой способ решения для других заданий похожего типа.

Вероятность того, что мотор холодильника прослужит более 1 года, равна 0,8, а вероятность того, что он прослужит более 2 лет, равна 0,6. Какова вероятность того, что мотор прослужит более 1 года, но не более 2 лет?

Вероятность того, что новый тостер прослужит больше года, равна 0,93. Вероятность того, что он прослужит больше двух лет, равна 0,82. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.

Источник

Непрерывная случайная величина

Ранее мы представили примеры решений задач о дискретной случайной величине, теперь переходим к непрерывной. Формально в задачах требуется найти тоже самое: вычислить числовые характеристики, начертить графики, определить неизвестные параметры, найти вероятности событий.

Но формулы-то совсем другие (в силу непрерывности СВ), поэтому стоит разобраться в них хорошенько. Надеемся, наши примеры вам помогут (а если нет времени, закажите решение).

Ниже вы найдете примеры решений на самые разные законы распределений непрерывных случайных величин: законы $\arcsin$ и $\arctan$, тригонометрические и логарифмические функции, показательный, равномерный закон распределения, законы Коши, Симпсона, Лапласа и т.д.

Примеры решений

Задача 1. Случайная величина X задана дифференциальной функцией распределения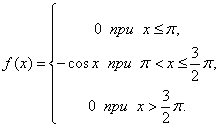

1) Определить вероятность попадания случайной величины X в интервал $[\pi, 5/4 \pi]$.
2) Найти математическое ожидание и дисперсию случайной величины X.

Задача 2. Случайная величина X задана плотностью вероятности: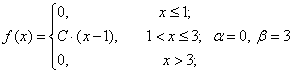

Требуется:
а) найти коэффициент C;
б) найти функцию распределения F(x);
в) найти M(X), D(X), σ(X)
г) найти вероятность P(α -2t при t ≥ 0 и f(t)=0 при t Решебник по теории вероятности онлайн

Больше 11000 решенных и оформленных задач по теории вероятности:

Источник

Непрерывная случайная величина

Ранее мы представили примеры решений задач о дискретной случайной величине, теперь переходим к непрерывной. Формально в задачах требуется найти тоже самое: вычислить числовые характеристики, начертить графики, определить неизвестные параметры, найти вероятности событий.

Но формулы-то совсем другие (в силу непрерывности СВ), поэтому стоит разобраться в них хорошенько. Надеемся, наши примеры вам помогут (а если нет времени, закажите решение).

Ниже вы найдете примеры решений на самые разные законы распределений непрерывных случайных величин: законы $\arcsin$ и $\arctan$, тригонометрические и логарифмические функции, показательный, равномерный закон распределения, законы Коши, Симпсона, Лапласа и т.д.

Примеры решений

Задача 1. Случайная величина X задана дифференциальной функцией распределения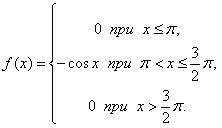

1) Определить вероятность попадания случайной величины X в интервал $[\pi, 5/4 \pi]$.
2) Найти математическое ожидание и дисперсию случайной величины X.

Задача 2. Случайная величина X задана плотностью вероятности: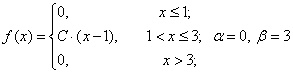

Требуется:
а) найти коэффициент C;
б) найти функцию распределения F(x);
в) найти M(X), D(X), σ(X)
г) найти вероятность P(α -2t при t ≥ 0 и f(t)=0 при t Решебник по теории вероятности онлайн

Больше 11000 решенных и оформленных задач по теории вероятности:

Источник

Числовые характеристики случайных величин

1. Математическое ожидание — характеристика центра группирования случайных величин:

– для дискретных случайных величин:

(2.27)

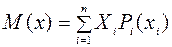
– для непрерывных случайных величин:

(2.28)

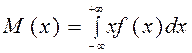
2. Дисперсия есть сумма произведений квадратов разностей случайных величин и математических ожиданий

– для дискретных случайных величин:

(2.29)

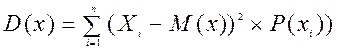
– для непрерывных случайных величин:

(2.30)

3. Среднее квадратическое отклонение:

(2.31)

(2.32)

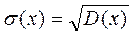
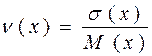
если: n(х) 0,33 – большое значение коэффициента.

Свойства математического ожидания:

Пример 2.1. Закон распределения случайной величины задан в виде таблицы:

Определить числовые характеристики случайных величин.

D(х) = (1 – 2,3) 2 ´ 0,3 + (2 – 2,3) 2 ´ 0,5 + (5 – 2,3) 2 ´ 0,2 » 2

Пример 2.2: Функция распределения имеет вид:

0, при х £ 0

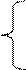
Оценить количественно, что вероятность примет значение из диапазона (0,5; 1). Какова вероятность попадания случайной величины в диапазон (0,5; 1) при условии, что событие не появится.

Контрольные вопросы и задачи

1. Почему надёжность необходимо рассматривать в вероятностном аспекте?

2. Как можно подсчитать вероятность безотказной работы через число отказавших объектов и общее число объектов?

3. Какими способами задаются случайной величины?

4. Перечислите и поясните основные теоремы вероятности.

5. Назовите следствия основных теорем теории вероятностей.

6. Закон распределения случайной величины задан в виде таблицы

Найти D(x), a, 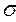(x), r(x), M(x 2 ).

7. Функция распределения имеет вид:

0, при x 0

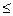
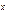
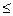
f(x) = e , при 0 x 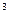1/2

x , при ½ 1

Найти вероятность того, что вероятность примет значение из диапазона

8. Прибор работает в двух режимах: «1» и «2». Режим «1» наблюдается в 60% случаев, режим «2» – в 40% случаев за время работы T. В режиме «1» прибор отказывает с вероятностью, равной 0,3, а в режиме «2» с вероятностью 0,5. Определить вероятность отказа прибора за время T. Ответ: 0,38.

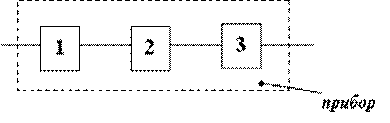
9. Прибор состоит из 3-х блоков, которые независимо друг от друга могут отказать. Отказ каждого из блоков приводит к отказу всего прибора. Вероятность того, что за время T работы прибора откажет первый блок, равна 0,15, второй – 0,25, третий – 0,1. Найти вероятность того, что за время T прибор проработает безотказно.

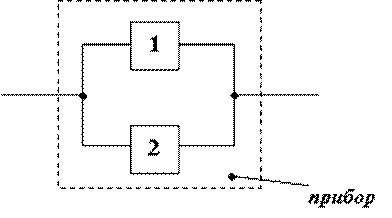
10. Прибор состоит из 2-х блоков, дублирующих друг друга. Вероятность того, что за время T каждый из блоков проработает безотказно, равна 0,9. Отказ прибора произойдет при отказе обоих блоков. Найти вероятность того, что за время T прибор проработает безотказно.

3 Показатели надёжности объекта

Безотказность и другие свойства надёжности проявляются через случайные величины: наработку до отказа (наработку между отказами) и количество отказов за заданное время. Поэтому количественными характеристиками здесь выступают вероятностные переменные.

Наработка – продолжительность (объём) работы объекта. Измеряется в любых неубывающих величинах (единица времени, число циклов нагружений, километры пробега и т. п.). Объект может работать непрерывно (с учётом перерывов на ремонт) или с перерывами, независящими от технического состояния (в этом случае различаются непрерывная и суммарная наработка).

Появление отказов не предопределено заранее, случайно, поэтому теория надежности основана на математическом аппарате теории вероятностей и математической статистики.

Для оценки надёжности проводятся эксплуатационные испытания значительного числа N элементов в течение времени t. Пусть к концу испытаний остается N_р работоспособных элементов и n отказавших.

Тогда относительное количество отказов:

. (3.1)

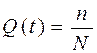
Вероятность безотказной работы оценивается относительным количеством работоспособных элементов:

. (3.2)

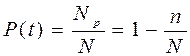
Вероятность безотказной работы (ВБР) означает, что в пределах заданной наработки отказ объекта не возникнет.

Так как безотказная работа и отказ – взаимно противоположные события, то сумма их вероятностей равна единице:

=F(t).

F(t) есть интегральная функция распределения случайной наработки t.

Так как события, заключающиеся в том, что наступил или не наступил отказ к моменту наработки t, являются противоположными, то нетрудно убедиться, что P(t) является убывающей, а Q(t) – возрастающей функцией наработки. Действительно, а) в момент начала испытаний t = 0 число работоспособных объектов равно общему их числу N(t) = N(0) = N, а число отказавших –

б) при наработке t ∞ все объекты, поставленные на испытания, откажут, то есть

Вероятность безотказной работы есть количественная мера того, что случайная величина наработки до отказа T окажется не меньше некоторой заданной наработки t, если t ≥0:

Очевидно, что Q(t) является функцией распределения случайной величины T и представляет собой вероятность того, что наработка до отказа окажется меньше некоторой заданной наработки t:

Q(t) = P<T 1 . (3.20)

Отсутствие последствия означает, что вероятность наступления n отказов в течение промежутка Δt_i не зависит от того, сколько было отказов и как они распределялись до этого промежутка. Следовательно, факт отказа любого элемента в системе не приведет к изменению характеристик (работоспособности) других элементов системы, если даже система и отказала из-за какого-то элемента.

Опыт эксплуатации сложных технических систем показывает, что отказы элементов происходят мгновенно и если старение элементов отсутствует

(l = const), то поток отказов в системе можно считать простейшим.

Случайные события, образующие простейший поток, распределены по закону Пуассона:

при n _і ³ 0 (3.21)

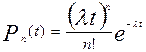
где Р_n(t) – вероятность возникновения в течение времени t ровно n событий (отказов); l – параметр распределения, совпадающий с параметром потока событий.

Если в выражении (2.16) принять n = 0, то получится 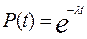– вероятность безотказной работы объекта за время t при интенсивности отказов

l = const. Нетрудно доказать, что если восстанавливаемый объект при отсутствии восстановления имеет характеристику l = const, то, придавая объекту восстанавливаемость, следует записать μ(t) = const; l = μ .

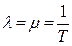
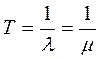
Это свойство широко используется в расчётах надёжности ремонтируемых устройств. Например, важнейшие показатели надежности оборудования электроустановок даются в предположении, что потоков отказов и восстановлений являются простейшими, когда и, соответственно,

. (3.22)

Среднее время восстановления Т _В:

, (3.23)

где n – число отказов объекта;

Т_Вi – время, затраченное на отыскание и устранение одного отказа.

, (3.24)

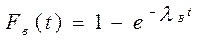
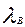
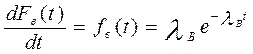
где – интенсивность восстановления работоспособности объекта; характеризует среднее число восстановлений ремонтируемого объекта в единицу времени,

. (3.25)

Интенсивность восстановления работоспособности объекта:

. (3.26)

, (3.27)

(3.28)

, (3.29)

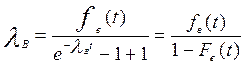
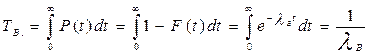
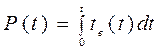
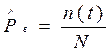
где n(t) – число восстановленных за время t объектов;

N – общее число отказавших объектов.

Вероятность безотказной работы восстанавливаемого объекта:

P_r(t) – количественная мера того, что объект в заданный момент времени будет работоспособен.

Событие А: объект работоспособен до момента времени t и работоспособен на участке времени Dt.

Событие В: объект вышел из строя к моменту времени t, но был восстановлен за период D t. Выражение для события В:

Согласно формулам (3.10) … (3.14)

,

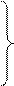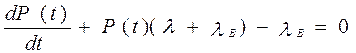
Решение этого дифференциального уравнения имеет вид:

. (3.31)

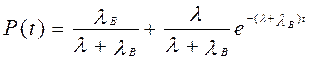
Изображение функции P_r(t) восстанавливаемого изделия и функции P(t) невосстанавливаемого изделия представлено на рисунке 3.2.

P(t)

Надёжность восстанавливаемого P_r(t) изделия всегда выше надёжности невосстанавливаемого изделия P(t).

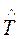
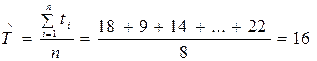
Пример 3.2. В результате наблюдения за работой редуктора было зарегистрировано 8 отказов, наработки t_i составляют в сутках 18, 9, 14, 27, 16, 8, 14, 22. Определить наработку на отказ и вероятность его безотказной работы в пределах наработки Dt = 20 ч.

суток

Источник