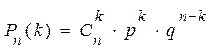Прибор состоит из трех узлов работающих независимо

Задача 52213 Устройство состоит из трех независимо.

Условие

Устройство состоит из трех независимо работающих элементов.
Вероятность отказа каждого элемента в одном опыте равна 0,3.
Составить закон распределения числа отказавших элементов в одном
опыте. Построить функцию распределения и ее график.

Все решения

Пусть случайная величина Х — число отказавших элементов в одном опыте.
Элементов три.
p=0,3 — вероятность отказа каждого элемента в одном опыте
q=1-p=0,7 — вероятность того, что в одном опыте элемент не откажет

Случайная величина Х может принимать значения от 0 до 3

p_(0) = C^(0)_(3)p^(0)*q^(3) — вероятность того, что в одном опыте откажут 0 элементов
p_(0)=1*0,3^(0)*0,7^3=0,343

p_(1) = C^(1)_(3)p^(1)*q^(2) — вероятность того, что в одном опыте откажет 1 элемент
p_(1)=3*0,3*0,7^2=0,441

p_(2) = C^(2)_(3)p^(2)*q^(1) — вероятность того, что в одном опыте откажут 2 элемента
p_(2)=3*0,3^2*0,7=0,189

p_(3) = C^(3)_(3)p^(3)*q^(0) — вероятность того, что в одном опыте откажут 0 элементов
p_(3) = 1*0,3^3*0,7^(0)=0,027

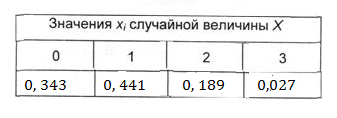
Закон распределения — таблица, в которой указаны значения случайной величины и их вероятности.

Сумма вероятностей должна быть равна 1. Это так
0,343+0,441+0,189+0,027=1

Закон составлен правильно.

0,343+0,441=0,784
0,784+0,189=0,973
0,973+0,027=1

График, ступенчатая функция

Источник

Схема Бернулли. Формула Бернулли

1. Схема Бернулли. Формула Бернулли

Пусть производится n независимых однотипных испытаний, в каждом из которых событие А может появиться с вероятностью Р. Тогда вероятность непоявления события А, т.е. Р( 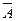) равна q=1-p.

Вероятность того, что событие А произойдет в этих n независимых испытаниях ровно k раз, можно вычислить по формуле Бернулли

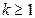
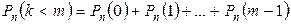
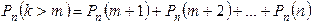
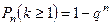
Для определения вероятности появления события A менее m раз (k m), хотя бы один раз ( ) и т. п. могут быть использованы формулы:

,

,

.

Пример: Прибор состоит из пяти узлов. Надежность (вероят­ность безотказной работы в течение времени t ) для каждого узла равна 0,9. Узлы выходят из строя независимо один от друго­го. Найти вероятность того, что за время t откажут ровно два узла.

Решение: Рассмотрим событие А — выход узла из строя за время t. Число узлов n=5. Число отказавших узлов за время t: k=2.

Р(А) — вероятность выхода узла из строя: p =P(A)=0,1. Тогда q=1-p=1-0,1=0,9.

Теперь вычислим искомую вероятность по формуле Бернулли:

Р₅(2) = 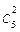(0,1) 2 . (0,9) 3 =10 . 0,01 . 0,729=0,0729.

Пример .Всхожесть семян данного растения равна 90 %. Найти вероятность того, что из четырех посеянных семян взойдут: а) три; б) не менее трех.

а) Искомую вероятность находим с помощью формулы Бернулли (14), учитывая что , , , .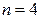

.

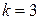
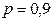
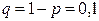
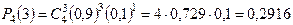
б) «Не менее трех» означает, что из четырех семян взойдут или три, или четыре. Так как эти события несовместны, то по теореме сложения искомая вероятность равна

.

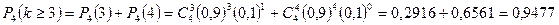
Источник

Учебник по теории вероятностей

1.9. Формула Пуассона

При большом числе испытаний $n$ и малой вероятности $р$ формулой Бернулли пользоваться неудобно, например, $0.97^<999>$ вычислить трудно. В этом случае для вычисления вероятности того, что в $n$ испытаниях ($n$ – велико) событие произойдет $k$ раз, используют формулу Пуассона:

Здесь $\lambda=n \cdot p$ обозначает среднее число появлений события в $n$ испытаниях.

Эта формула дает удовлетворительное приближение для $p \le 0,1$ и $np \le 10$. Cобытия, для которых применима формула Пуассона, называют редкими, так как вероятность их осуществления очень мала (обычно порядка 0,001-0,0001).

При больших $np$ рекомендуется применять формулы Лапласа (Муавра-Лапласа).

Примеры решений на формулу Пуассона

Пример. Устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течении времени Т равна 0,002. Найти вероятность того, что за время Т откажут ровно три элемента.

Решение. По условию дано: $n=1000$, $p=0,002$, $\lambda=np=2$, $k=3$.

Искомая вероятность после подстановки в формулу:

Пример. Завод отправил на базу 500 изделий. Вероятность повреждения изделия в пути 0,004. Найти вероятность того, что в пути повреждено меньше трех изделий.

Решение. По условию дано: $n=500$, $p=0,004$, $\lambda=np=2$.

По теореме сложения вероятностей получаем вероятность того, что повреждено меньше 3 изделий, то есть 0, 1 или 2 изделия:

Пример. Магазин получил 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0,003. Найти вероятность того, что магазин получит более двух разбитых бутылок.

Решение. По условию дано: $n=1000$, $p=0,003$, $\lambda=np=3$.

Чтобы найти вероятность $P_<1000>(k\gt 2)$ того, что магазин получит более двух разбитых бутылок, используем переход к противоположному событию (разбито не более 2 бутылок, то есть 0, 1 или 2):

$$ P_<1000>(k\gt 2) = 1 — P_<1000>(k\le 2) = 1 — (P_<1000>(0)+P_<1000>(1)+P_<1000>(2)) = \\=1 — \left(\frac<3^0><0!>\cdot e^ <-3>+ \frac<3^1><1!>\cdot e^ <-3>+ \frac<3^2><2!>\cdot e^ <-3>\right) =\\ =1 — \left(1 + 3 + 9/2 \right)\cdot e^ <-3>\approx 0,568. $$

Видео о решении задач с помощью формулы Пуассона

Подробную статью о формуле с примерами, онлайн калькулятор и расчетный файл к видеоролику вы найдете тут.

Источник

05. Примеры решения задач

Задача 1. Каждый из четырех студентов, проживающих в одной комнате общежития, может присутствовать или не присутствовать на лекции по теории вероятностей. Рассматриваются события:

A — На лекции присутствует ровно один из четырех студентов ;

B — На лекции присутствует хотя бы один из четырёх студентов;

C — На лекции присутствуют не менее двух из четырех студентов;

D — На лекции присутствуют ровно два из четырех студентов;

E — На лекции присутствуют ровно три из четырех студентов;

F — На лекции присутствуют все четыре студента.

Решение: Начинать решение нужно с построения пространства элементарных исходов (элементарных событий) рассматриваемого эксперимента. Вспомним, что таким пространством называется любое множество W взаимоисключающих исходов эксперимента такое, что каждый интересующий нас результат эксперимента может быть однозначно описан с помощью элементов этого множества. В данном случае случайный эксперимент заключается в наблюдении за четырьмя студентами и выяснении, посещают ли они лекции по теории вероятностей. Нас интересует только количество студентов, присутствующих на лекции. Пусть элемент описывает элементарный исход, означающий, что на лекции присутствовало ровно i студентов. Тогда Все случайные события формально есть подмножества множества описаний элементарных исходов. Выпишем формально все события, о которых идет речь в условии задачи. Для этого нужно перечислить описания элементарных исходов, благоприятствующих каждому из этих событий. Таким образом будем иметь: Применяя теоретико-множественные операции для множеств получим ответ задачи. Ответ: а)

Г)

Е)

Задача 2. Пусть прибор состоит из трех блоков первого типа и двух блоков второго типа. Для того, чтобы прибор работал нормально необходима исправность хотя бы двух блоков первого типа и хотя бы одного блока второго типа. Пусть события означают исправность блока первого типа при События означают исправность блока второго типа при Используя теоретико-множественные операции записать событие , означающее что прибор исправен.

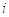
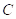
Решение: Для наступления события 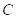на самом деле необходимо наступление двух событий . Событие значит, что исправны хотя бы два блока первого типа. Событие значит, что исправен хотя бы один блок второго типа. Таким образом получим Осталось записать события И . Событие Наступает в случае, если одновременно наступают и , т. е. имеет место событие Ç, или если одновременно появятся И , или одновременно наступают и . При этом не исключается случай одновременного наступления всех трех событий , и . Таким образом используя определения операций объединения и пересечения событий, получим Заметим, что событие , означающее одновременное появление , и , содержится в каждом из трех объединяемых событий в выражении для . Аналогично запишем Ответ: .

Задача 3. Используя законы для операций над событиями доказать справедливость следующего равенства:

Решение. Пользуясь свойством г) для операций над событиями запишем: Далее, используя закон де Моргана и первый распределительный закон, получим:

Что и требовалось доказать.

Задача 4. Используя определения операций над событиями доказать, что .

Решение: Для решения задачи достаточно показать выполнение двух включений: 1) Докажем первое включение, второе доказывается аналогично. Будем предполагать, что в противном случае первое включение очевидно. Выберем некоторый элементарный исход Покажем, что тогда Пусть Тогда по определению разности событий запишем:

. Далее по определению операции пересечения событий и получаем, что Что и требовалось доказать.

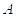
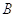
Источник