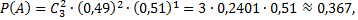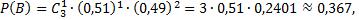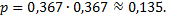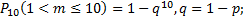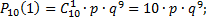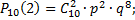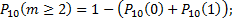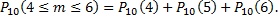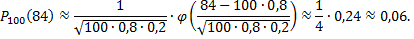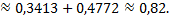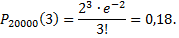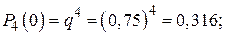Занятие №48. Повторные независимые испытания
№1. В семье трое детей. Какова вероятность того, что: а) все они мальчики; б) один мальчик и две девочки. Считать вероятность рождения мальчика 0,51, а девочки – 0,49.
Примечание: a) в данном случае используем формулу Бернулли, учитывая, что 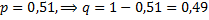
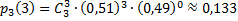
б) Искомая вероятность находится по теореме умножения, так как интересует одновременное появление событий: 
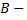

№2. Прибор состоит из 10 узлов. Надежность (вероятность безотказной работы в течении времени 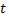
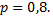
а) откажет хотя бы один узел;
б) откажет ровно один узел;
г) откажут не менее двух узлов;
д) откажут от 4 до 6 узлов.
Примечание: a)
б)
в)
г)
д)
№3. Вероятность наступления события 

б) не менее 72 и не более 84 раза.
Примечание: задача состоит в том, что необходимо найти вероятность появления определенного количества интересующих исходов (84) из всех возможных исходов (100). Так как общее число испытаний достаточно велико, то стоит применить формулу Лапласа для нахождения вероятности
Аналогичные рассуждения указывают на решение второй части вопроса, применяя интегральную формулу Лапласа:
№4. Задачник по теории вероятностей издан тиражом 20 000 экземпляров. Вероятность того, что он сброшюрован неправильно, равна 0,0001. Найти вероятность того, что тираж содержит три бракованных книги.
Применение: в данном случае вероятность появления интересующего исхода очень мала, а количество проведенных испытаний достаточно велико. Следует проверить, возможно ли использовать формулу Пуассона: 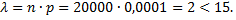
№5. Найти вероятность того, что в партии из 900 изделий число изделий высшего сорта заключено между 600 и 700. Вероятность появления изделия высшего сорта в партии равна 0,8.
№6. Завод отправил на базу 10 000 стаканов. Стаканы разбиваются в пути с вероятностью 0,0002. Какова вероятность того, что в пути разобьется менее трех стаканов?
№7. Среди 5000 семян 0,03% сорняков. Найти вероятность того, что будет найдено не менее двух семян сорняков.
№8. Прибор состоит из 200 деталей, каждая из которых может выйти из строя с вероятностью 0,01. Найти вероятность того, что выйдут из строя не более трех деталей.
№9. На опытной станции посеяно 150 семян кукурузы. Всхожесть семян 95%. Найти вероятность того, что из 150 семян взойдет не менее 90%.
№10. Завод отправил на базу 5000 изделий. Вероятность того, что в пути изделие повредится, равна 0,0002. Найти вероятность того, что на базу прибудет 3 поврежденных изделия.
Источник
Общая теорема о повторении опытов
Если производится 


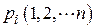





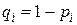
Прибор состоит г из 10 узлов. Надежность (вероятность безотказной работы в течение времени 


а) откажет хотя бы один узел;
б) откажет ровно один узел;
г) откажет не менее двух узлов.
а) 
б) 
в) 
г) 
В урне 30 белых и 15 черных шаров. Вынули подряд 5 шаров, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Какова вероятность того, что из 5 вынутых шаров окажется 3 белых.
Вероятность извлечения белого шара 


Ответ: 
Монету подбрасывают восемь раз. Какова вероятность того, что шесть раз она упадет гербом вверх?
Имеем схемуиспытаний Бернулли. Вероятность появления Ге в одном испытании 

Производится четыре независимых выстрела, причем 
Найти вероятности: 
Найдем
По формуле Бернулли имеем
Имеется пять станций, с которыми поддерживается связь. Время от времени связь прерывается из-за атмосферных помех. Вследствие удаленности станций друг от друга перерыв связи с каждой из них происходит независимо от остальных с вероятностью 0,2. Найти вероятность того, что в данный момент времени будет поддерживаться связь не более чем с двумя станциями.
Событие 
Система радиолокационных станций ведет наблюдение за группой объектов, состоящей из десяти единиц. Каждый из объектов может быть (независимо от других) потерян с вероятностью 0,1. Найти вероятность того, что хотя бы один из объектов будет потерян.
Вероятность потери хотя бы одного объекта 

но проще воспользоваться вероятностью противоположного события – ни один объект не потерян – и вычесть ее из единицы

Варианты заданий для контрольной работы № 5
1. Подброшены две игральные кости. Найти вероятность того, что сумма выпавших очков равна 7.
2. Пусть 
3. Монету бросают 5 раз. Найти вероятность того, что «герб» выпадет: а) не менее двух раз, б) менее двух раз.
4. Имеются 2 одинаковые урны. В первой урне находятся 3 белых и 5 чёрных шаров, во второй – 3 белых и 7 чёрных шаров. Из одной наугад выбранной урны извлекается шар. Определить вероятность того, что шар
чёрный.
5. В чемпионате страны по футболу участвуют 18 команд, Каждые две команды встречаются на футбольных полях 2 раза. Сколько матчей играется в сезоне?
1. Набирая номер телефона, абонент забыл последние 3 цифры, и помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что, набраны нужные цифры.
2. Верно ли 
3. Найти вероятность того, что событие 

4. Электрические приборы поставляются в магазин тремя заводами. Первый поставляет 50 %, второй – 20 %, третий – 30 % всей продукции. Вероятности изготовления прибора высшего качества каждым заводом, соответственно равны: 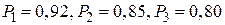
5. Буквы азбуки Морзе образуются как последовательность точек и
тире. Сколько различных букв можно образовать, если использовать 5
символов?
1. В ящике 10 пронумерованных шаров с номерами от 1 до 10. Вынули один шар. Какова вероятность того, что номер вынутого шара не превышает 10.
2. Верно ли равенство 
3. Вероятность наступления события 

4. Имеются три одинаковые урны. В первой урне находятся 5 белых и 5 чёрных шаров, во второй – 3 белых и 2 чёрных шара, в третьей – 7 белых и 3 чёрных. Из одной наугад выбранной урны извлекается шар. Определить вероятность того, что шар будет белый.
5. Сколькими способами можно разместить 12 человек за столом, на котором поставлено 12 приборов.
1. В цехе работает 6 мужчин и 4 женщины. По табельным номерам наудачу выбраны 7 человек. Найти вероятность того, что среди отобранных лиц окажется 3 женщины.
2. Доказать, что 
3. Пусть вероятность того, что наудачу взятая деталь нестандартная, равна 0,1. Найти вероятность того, что среди взятых наудачу 5 деталей не более двух нестандартных.
4. Имеются три одинаковые урны. В первой урне находятся 3 белых и 3 чёрных шаров, во второй – 2 белых и 6 чёрных шаров, в третьей – 5 белых и 2 чёрных. Из одной наугад выбранной урны извлекается шар. Определить вероятность того, что шар будет чёрный.
5. Требуется составить расписание отправления поездов на различные дни недели. При этом необходимо, чтобы: 3 дня отправлялись 2 поезда в день, 2 дня – по 1 поезду в день, 2 дня – по 3 поезда в день. Сколько можно составить различных расписаний?
1. Куб, все грани которого окрашены, распилен на 64 кубика одинакового размера, которые затем перемешаны. Найти вероятность того, что случайно извлечённый кубик имеет две окрашенные грани.
2. Доказать, что 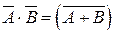
3. Пусть вероятность того, что телевизор потребует ремонта в течение гарантийного срока, равна 0,2. Найти вероятность того, что в течение гарантийного срока из 6 телевизоров: а) не более 1 потребует ремонта, б) хотя бы 1 не потребует ремонта.
4. На трёх автоматических линиях изготавливаются однотипные детали. Вследствие разладки станков возможен выпуск бракованной продукции: первой линией с вероятностью 0,02; второй – с вероятностью 0,01; третьей – с вероятностью 0,05. Первая линия даёт 70 %, вторая – 20 %, третья – 10 % всей продукции. Определить вероятность получения брака.
5. В урне 
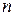
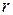

1. В урне 12 шаров: 3 белых, 4 чёрных и 5 красных шаров. Какова вероятность вынуть из урны красный шар.
2. Доказать, что 
3. Вероятность выиграть по лотерейному билету равна 
4. В двух ящиках лежат однотипные детали: в первом ящике 8 исправных и 2 бракованные, во втором 6 исправных и 4 бракованные. Из первого ящика наугад взяты две детали, а из второго одна деталь. Детали, перемешав, поместили в третий ящик, откуда наугад взяли одну деталь. Определить вероятность того, что эта деталь исправна.
5. Сколькими способами из колоды в 36 карт можно выбрать 2 карты пик?
1. В урне 15 шаров с номерами от 1 до 15. Какова вероятность вынуть шар с номером 18?
2. Доказать, что 
3. Вероятность попадания при каждом выстреле равна 0,4. Найти вероятность разрушения объекта, если для этого необходимо не менее 3 попаданий, а сделано 15 выстрелов.
4. В двух одинаковых урнах имеется по 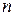

5. Из множества 
1. Внутри эллипса 

2. Пусть 



3. Найти вероятность того, что в семье, имеющей 6 детей, не менее
2 девочек. (Вероятности рождения мальчика и девочки считать одинаковые.)
4. Имеются две урны. В первой урне находятся 3 белых и 5 чёрных шаров, во второй – 4 белых и 6 чёрных шара. Из первой урны во вторую, не глядя, перекладывают два шара. Шары во второй урне тщательно перемешивают и из неё берётся один шар. Найти вероятность того, что шар будет
белый.
5. Сколькими способами можно обозначить вершины данного треугольника, используя буквы 
1. Из пяти букв разрезной азбуки, составлено слово «книга». Ребёнок, не умеющий читать, рассыпал эти буквы, а затем собрал в произвольном порядке. Найти вероятность того, что у него снова получилось слово «книга».
2. Найти все события 



3. Из 15 лотерейных билетов, выигрышными являются 4. Какова вероятность того, что среди 6 взятых наугад билетов будет два выигрышных?
4. Имеются три одинаковые урны. В первой урне находятся 4 белых и 2 чёрных шара, во второй – 3 белых и 3 чёрных шара, в третьей – 1 белых и 5 чёрных шаров. Из второй и третьей урн, не глядя, перекладывают по два шара в первую урну. Шары в первой урне перемешивают и из неё наугад извлекают два шара. Найти вероятность того, что они будут белые.
5. Из пяти шахматистов для участия в турнире нужно послать двух. Сколькими способами можно это сделать?
1. 

2. Даны два дублирующих блока 

3. Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0,95 для первого 0,9 – для второго. Найти вероятность того, что при аварии сработает только один сигнализатор.
4. На трёх автоматических линиях изготавливаются одноимённые детали. Первая линия даёт 70 %, вторая – 20 %, третья – 10 % всей продукции. Вероятности получения бракованной продукции на каждой линии, соответственно, равны: 0,02; 0,01; 0,05. Взятая на удачу деталь оказалась бракованной. Определить вероятность того, что деталь была изготовлена на первой линии.
5. На окружности выбрано 10 точек. Сколько можно провести хорд с концами в этих точках.
1. В урне 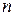


2. Верно ли равенство 
3. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно равна 0,9. Найти вероятность того, что из двух проверенных изделий только одно стандартное.
4. Три стрелка независимо один от другого стреляют по мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень для первого стрелка равна 0,4 для второго – 0,6 и для третьего – 0,7. После стрельбы в мишени обнаружены два попадания. Определить вероятность того, что они принадлежат первому и третьему стрелкам.
5. Сколькими способами можно расположить в 1 ряд 5 красных, 4 чёрных и 5 белых мячей так, чтобы мячи, лежащие на краях, были одного цвета?
1. Собрание, на котором присутствует 25 человек, в том числе 5 женщин, выбирает делегацию из 3 человек. Считая, что каждый из присутствующих с одинаковой вероятностью может быть избран. Найти вероятность того, что в делегацию войдут 2 женщины и один мужчина.
2. Обязаны ли совпадать события 

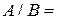

3. Найти вероятность 


4. По каналу связи может быть передан код 1111 с вероятностью 0,2, код 0000 с вероятностью 0,3 и код 1001 с вероятностью 0,5. Вследствие влияния помех вероятность правильного приёма каждой цифры (0 или 1) кода равна 0,9, причём цифры искажаются независимо друг от друга. Найти вероятность того, что передан код 1111, если на приёмном устройстве принят код 1011.
5. Сколько различных маршрутов может избрать пешеход, решивший пройти 9 кварталов, 5 из них – на запад, 4 – на север.
1. Группа из 10 мужчин и 10 женщин делится случайным образом на две равные части. Найти вероятность того, что в каждой части мужчин и женщин одинаково.
2. 


3. Найти вероятность 
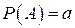
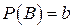

4. По линии связи возможна передача кода 1234 с вероятностью 0,6 и кода 4321 с вероятностью 0,4. Код высвечивается на табло, которое может исказить цифры. Вероятность принять 1 за 1 равна 0,8, а 1 за 4 равна 0,2. Вероятность принять 4 за 4 равна 0,9, а 4 за 1 равна 0,1. Вероятность принять 2 за 2 и 3 за 3 равна 0,7. Вероятность принятия 2 за 3 и 3 за 2 равна 0,3. Оператор принял код 4231. Определить вероятность того, что был принят код:
а) 1234; б) 4321.
5. Между тремя лицами – 



1. В партии из 10 изделий имеется 4 бракованных. Наугад выбирают
5 изделий. Определить вероятность того, что среди этих 5 изделий окажется три бракованных.
2. Доказать, что 


3. Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент ответит на 2 вопроса, предложеных ему экзаменатором.
4. Имеется 4 партии деталей. В первой партии 3 % брака, во второй –4 %, в третьей и четвёртой партиях брака нет. Какова вероятность взять бракованную деталь, если из выбранной наугад партии берётся одна деталь? Какова вероятность того, что взятая деталь принадлежит первой партии, если она оказалась бракованной?
5. Студенту необходимо сдать 4 экзамена в течение 10 дней. Сколькими способами можно составить ему расписание?
1. В зале 50 мест. Найти вероятность того, что из 10 человек 5 займут определённые места, если места занимаются ими случайным образом.
2. Доказать, что 
3. Три стрелка независимо друг от друга стреляют по цели. Вероятность попадания в цель для первого стрелка – 0,75, для второго – 0,8, для третьего – 0,9. Найти вероятность того, что все три стрелка попадут в цель.
4. Из урны, в которой имелось 4 чёрных 6 белых шаров, потерян шар неизвестного цвета. Для того чтобы определить состав шаров в урне, из неё наудачу извлекли два шара. Они оказались белыми. Найти вероятность того, что был утерян белый шар.
5. Сколькими способами можно расставить на полке 7 книг, если две определённые книги всегда должны стоять рядом.
1. В конверте 10 фотографий, среди которых две нужные. Извлечено 5 фотографий. Какова вероятность, что нужные две среди них.
2. Пусть 

3. Вероятности попадания в цель при стрельбе из трёх орудий соответственно равны: 


4. В ящике имеется 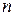

5. Цветочница продаёт розы четырёх разных сортов. Сколько разных букетов можно составить из дюжины роз?
1. В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов 5 отличников.
2. Обязаны ли совпадать события 



3. Бросаются две монеты. Рассматриваются события: 




4. Вероятность попадания в цель при одном выстреле равна 0,7. Определить вероятность того, что в результате шести независимых выстрелов будет пять попаданий.
5. В автомобиле 7 мест. Сколькими способами 7 человек могут усесться в эту машину, если занять место водителя могут только трое из них.
1. Для производственной практики на 30 студентов предоставлено 15 мест в Москве, 8 – в Тайге и 7 – в Новосибирске. Какова вероятность того, что два определённых студента попадут на практику в один город?
2. Пусть 


3. В ящике 6 белых и 8 чёрных шаров. Из ящика вынули два шара (не возвращая вынутый шар в ящик). Найти вероятность того, что оба шара белые.
4. Рабочий обслуживает 6 одинаковых станков. Вероятность того, что станок в течение некоторого промежутка времени потребует к себе внимания, равна 0,4. Найти вероятность того, что за время 
5. Нужно послать 6 писем. Сколькими способами можно сделать, если для доставки писем имеются три курьера?
1. Найти вероятность того, что при подбрасывании трёх игральных костей ровно на одной из них выпадет шестёрка.
2. Двое играют в шахматы. Событие 

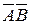
б) 

3. В первом ящике 2 белых и 10 чёрных шаров, во втором 8 белых и
4 чёрных шара. Из каждого ящика вынули по шару. Какова вероятность, что оба шара белые?
4. Испытываются 25 двигателей. Вероятность безотказной работы каждого двигателя одинакова и равна 0,95. Определить наиболее вероятное число отказавших двигателей.
5. У Тани есть 20 марок, у Наташи – 30. Сколькими способами можно обменять одну Танину марку на одну Наташину?
1. Бросают 4 игральные кости. Найти вероятность того, что на всех выпадает одинаковое число очков.
2. Обязаны ли совпадать события 

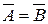
3. Три стрелка независимо друг от друга стреляют по цели. Вероятность попадания в цель для первого стрелка равна 0,75, для второго – 0,8. для третьего – 0,9. Определить вероятность того, что в цель попадёт хотя бы один стрелок.
4. Испытанию подвергается партия транзисторов. Вероятность безотказной работы каждого транзистора равна 0,92. Определить, какое число транзисторов следует испытать, чтобы с вероятностью не менее 0,95 можно было зафиксировать хотя бы один отказ.
5. Сколько пятизначных чисел можно составить из цифр 1, 2, 4, 6, 7, 8, если каждую цифру в любом числе использовать не более 1 раза?
Источник