Определить срок изготовления прибора информатика

Уроки 13 — 14
Использование графов
(§7. Системный подход в моделировании)

Содержание урока

Задачи с 1 по 8

Задачи с 1 по 8

1. В графе 9 узлов, причём каждый узел связан со всеми другими. Сколько всего связей в этой модели?

2. Система состоит из трёх подсистем по три элемента в каждой. Все элементы в каждой подсистеме связаны со всеми другими, кроме того, каждая подсистема связана со всеми другими подсистемами. Сколько всего связей в этой системе? Сравните ответы этой и предыдущей задач, сделайте выводы.

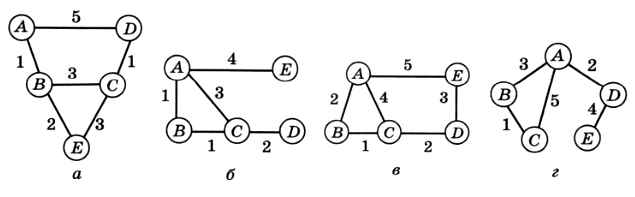
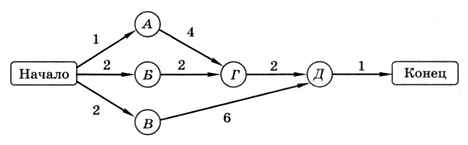
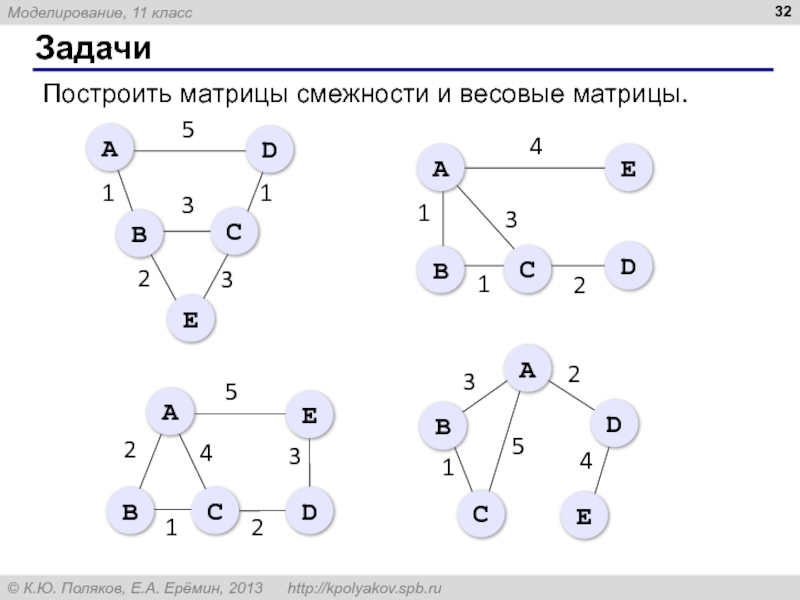
3. Постройте матрицы смежности и весовые матрицы для следующих графов.

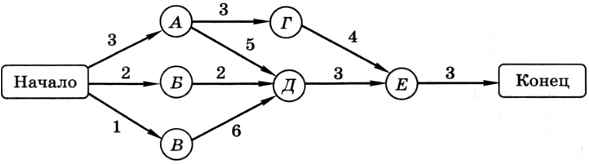
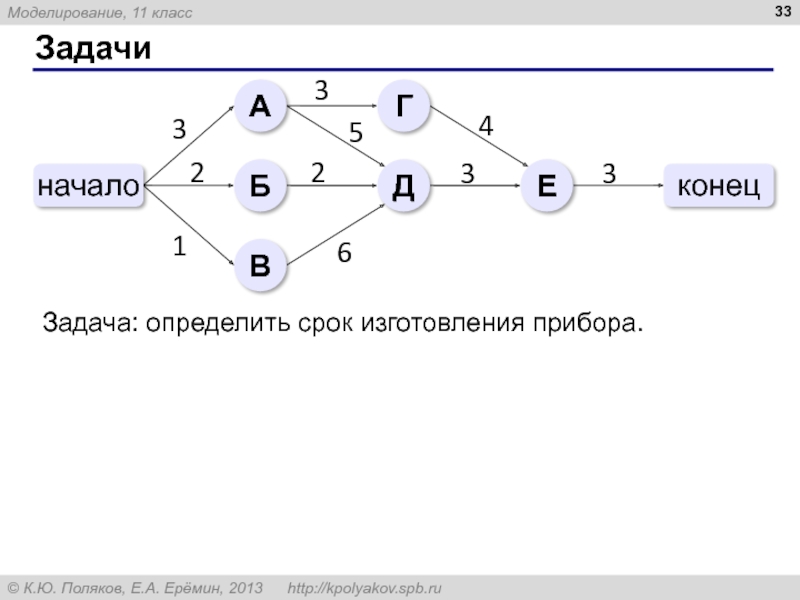
4. Изготовление прибора «Заря-М» описывается следующей сетевой моделью (веса дуг обозначают длительность работ в днях).

Определите, через сколько дней после начала работ будет изготовлен прибор.

5. Постройте семантическую сеть на основе текста: «Кошачьи — семейство млекопитающих отряда хищных. Кроме кошек к ним относятся, например, львы и тигры. У кошачьих развиты слух и зрение. У нас дома живёт кошка Мурка. У неё рыжая шерсть».

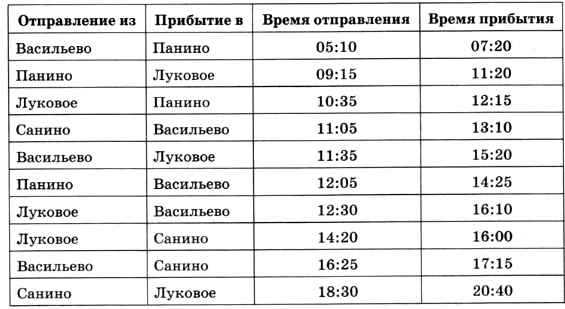
6. Путешественник прибыл в посёлок Луковое в полночь по местному времени и увидел следующее расписание автобусов.

Определите самое раннее время, когда он может попасть в Васильево, и как ему нужно ехать.

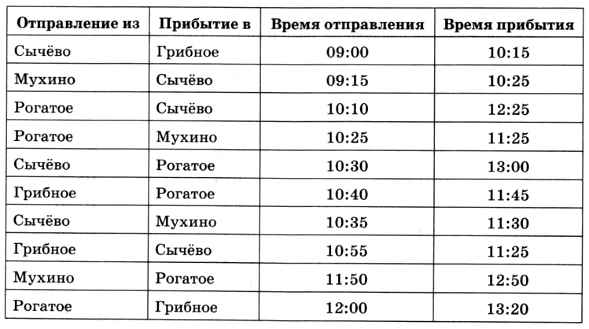
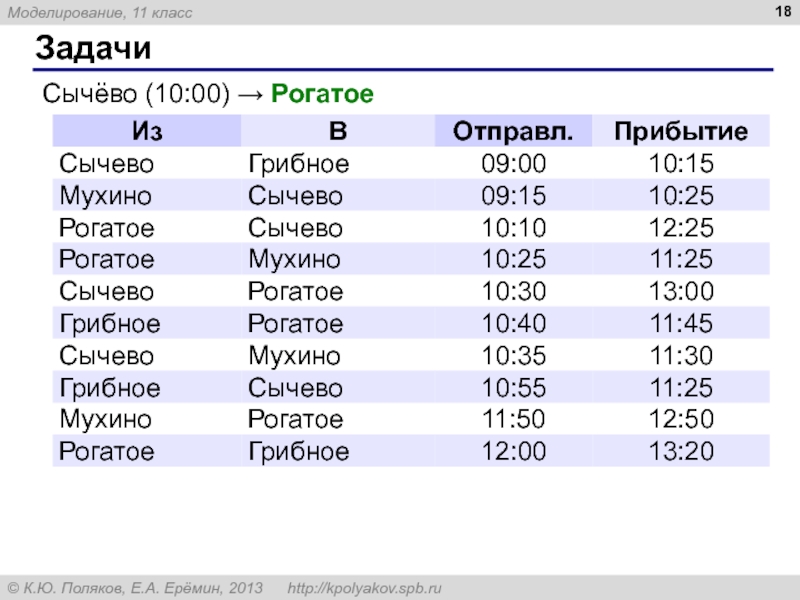
7. Путешественник прибыл в посёлок Сычёво в 10:00 по местному времени и увидел следующее расписание автобусов.

Определите самое раннее время, когда он может попасть в посёлок Рогатое, и как ему нужно ехать.

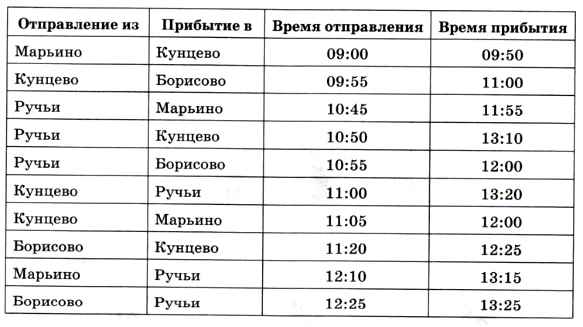
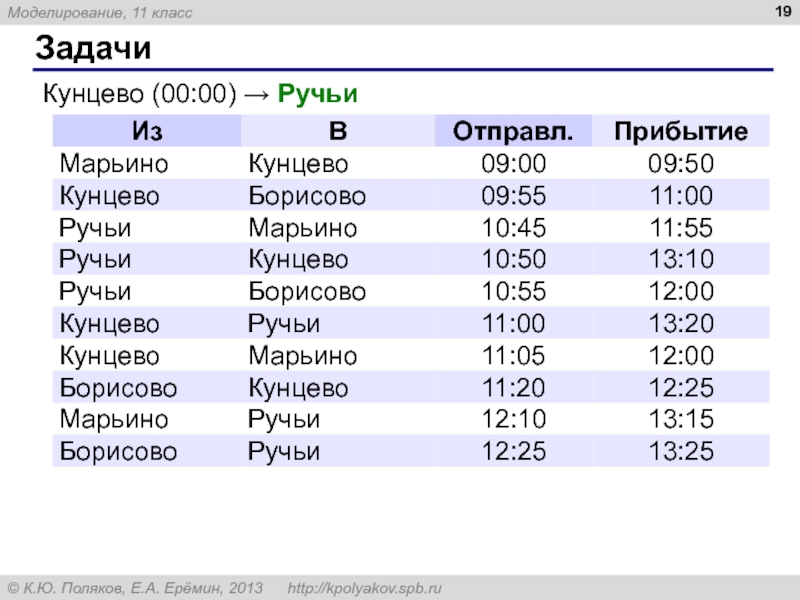
8. Путешественник прибыл в посёлок Кунцево в полночь по местному времени и увидел следующее расписание автобусов.

Определите самое раннее время, когда он может попасть в посёлок Ручьи, и как ему нужно ехать.

Следующая страница Задачи с 9 по 16

Источник

Уроки 13 — 14
Использование графов
(§7. Системный подход в моделировании)

Содержание урока

Сетевые модели

Сетевые модели

В сетевых моделях (графах) каждый узел может быть связан со всеми другими. Знакомые вам сетевые модели — это схемы дорог, компьютерных сетей, электрических цепей.

Графы позволяют очень наглядно представить информацию, однако они неудобны для автоматической обработки. Поэтому в памяти компьютера информация о графах обычно хранится в виде табличных моделей — матриц смежности и весовых матриц (вспомните материал учебника для 10 класса).

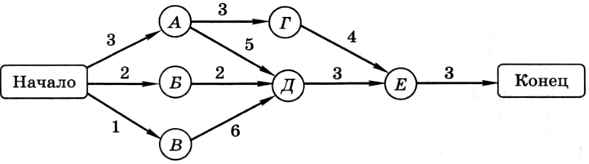
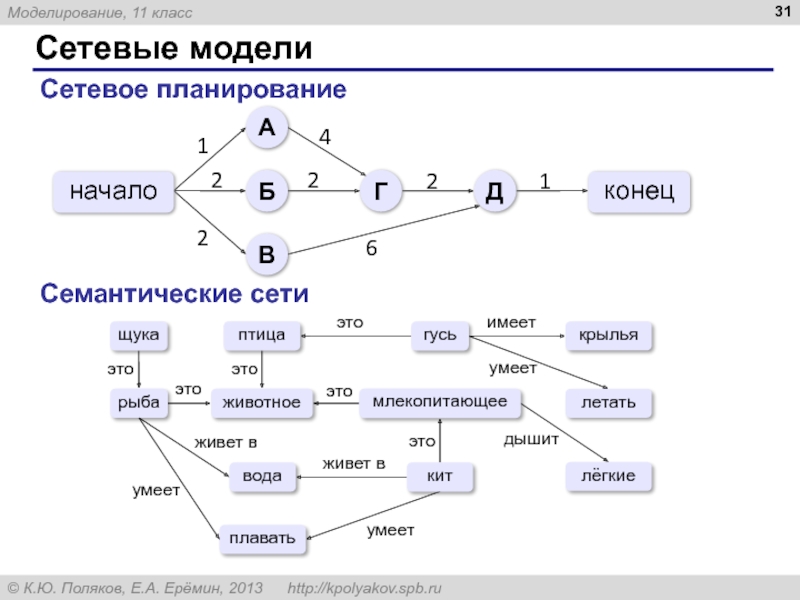
Сетевые модели широко применяются для планирования производства, есть даже специальный термин «сетевое планирование». Предположим, что изготовление аппарата МУХ-8-ККВ включает 8 операций, причём некоторые из них можно выполнять одновременно. Чтобы определить время изготовления, строят схему (граф, сеть), на которой узлы обозначают события (когда можно начинать очередную операцию), дуги — работы, а числа около дуг (веса) — длительность этих работ, например, в днях (рис. 2.10).

По этой схеме видно, что в самом начале можно выполнять три работы параллельно. Чтобы начать работу Г-Д, нужно закончить работы А-Г и Б-Г, на это требуется 5 дней. Чтобы выполнить последнюю операцию и получить готовое изделие, нужно закончить работы Г-Д и В-Д, на это требуется 8 дней. Поэтому аппарат будет готов только через 9 дней с момента начала работ.

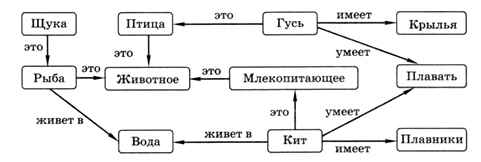
Для представления знаний применяют специальные сетевые модели, которые называются семантическими сетями (семантика изучает смысл сообщений). В них узлы — это объекты (понятия, процессы, явления), а дуги — связи (отношения) между ними (рис. 2.11).

Семантические сети наглядны, с их помощью удобно анализировать фразы на естественном языке, они соответствуют современным представлениям об организации памяти человека. Однако пока такие структуры плохо приспособлены для автоматической обработки информации и поиска решений.

Сейчас делаются попытки на основе сети Интернет создать семантическую паутину — распределённую базу знаний. Для этого в веб-страницы нужно будет добавить специальную смысловую информацию, понятную компьютерным системам (так называемые метаданные).

Следующая страница Игровые стратегии

Источник

Урок 8
Использование графов
(§7. Системный подход в моделировании)

Содержание урока

Задачи с 1 по 8

Задачи с 1 по 8

1. В графе 9 узлов, причём каждый узел связан со всеми другими. Сколько всего связей в этой модели?

2. Система состоит из трёх подсистем по три элемента в каждой. Все элементы в каждой подсистеме связаны со всеми другими, кроме того, каждая подсистема связана со всеми другими подсистемами. Сколько всего связей в этой системе? Сравните ответы этой и предыдущей задач, сделайте выводы.

3. Постройте матрицы смежности и весовые матрицы для следующих графов.

4. Изготовление прибора «Заря-М» описывается следующей сетевой моделью (веса дуг обозначают длительность работ в днях).

Определите, через сколько дней после начала работ будет изготовлен прибор.

5. Постройте семантическую сеть на основе текста: «Кошачьи — семейство млекопитающих отряда хищных. Кроме кошек к ним относятся, например, львы и тигры. У кошачьих развиты слух и зрение. У нас дома живёт кошка Мурка. У неё рыжая шерсть».

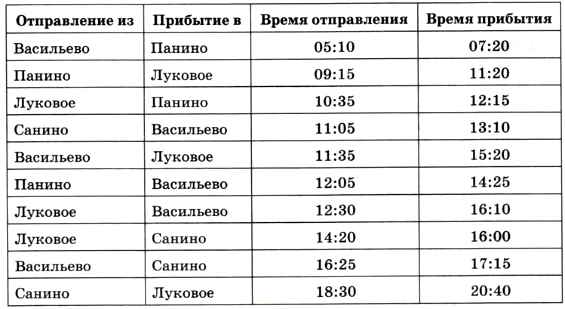
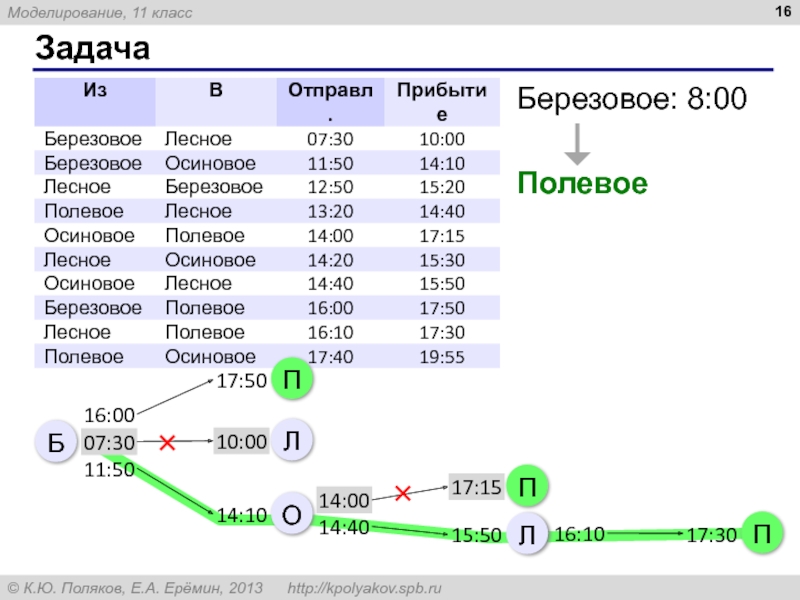
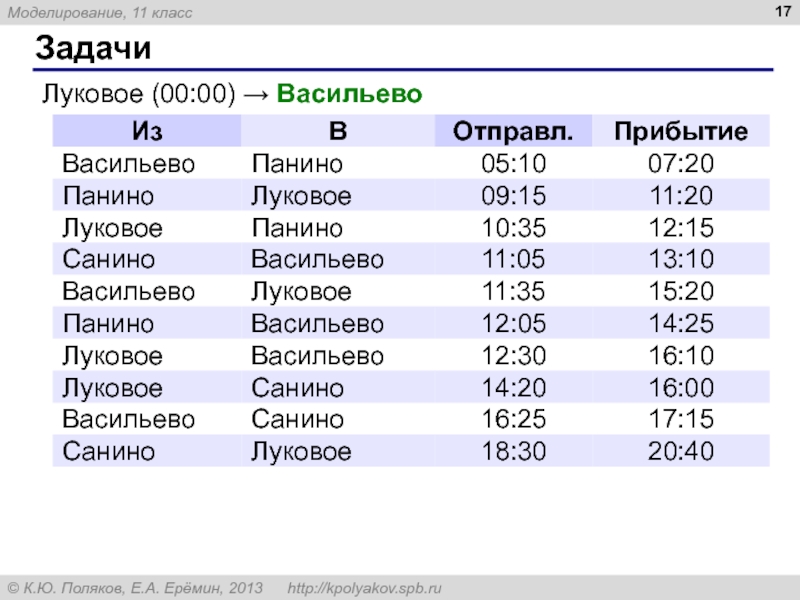
6. Путешественник прибыл в посёлок Луковое в полночь по местному времени и увидел следующее расписание автобусов.

Определите самое раннее время, когда он может попасть в Васильево, и как ему нужно ехать.

7. Путешественник прибыл в посёлок Сычёво в 10:00 по местному времени и увидел следующее расписание автобусов.

Определите самое раннее время, когда он может попасть в посёлок Рогатое, и как ему нужно ехать.

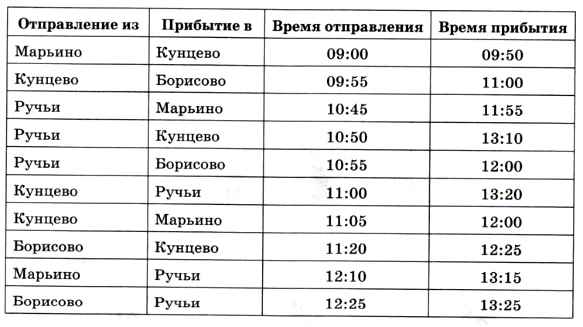
8. Путешественник прибыл в посёлок Кунцево в полночь по местному времени и увидел следующее расписание автобусов.

Определите самое раннее время, когда он может попасть в посёлок Ручьи, и как ему нужно ехать.

Следующая страница Задачи с 9 по 16

Источник

Учитель информатики

Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.

Системный подход в моделировании. ГДЗ по Информатике 11 класс.

Информатика. 11 класс. Углубленный уровень. В 2 ч. Поляков К.Ю., Еремин Е.А.

§ 7. Системный подход в моделировании

1. Приведите примеры, когда в одной и той же ситуации люди используют разные модели. Какие из них можно считать системами?
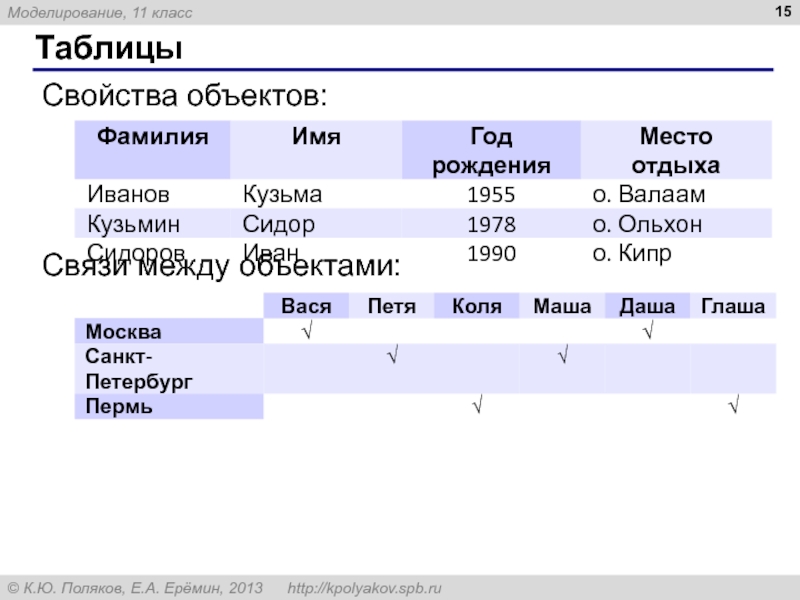
2. Какие два типа табличных моделей вы знаете?
3. К какому типу можно отнести модель, построенную при решении задачи с путешественником? Обоснуйте ответ.
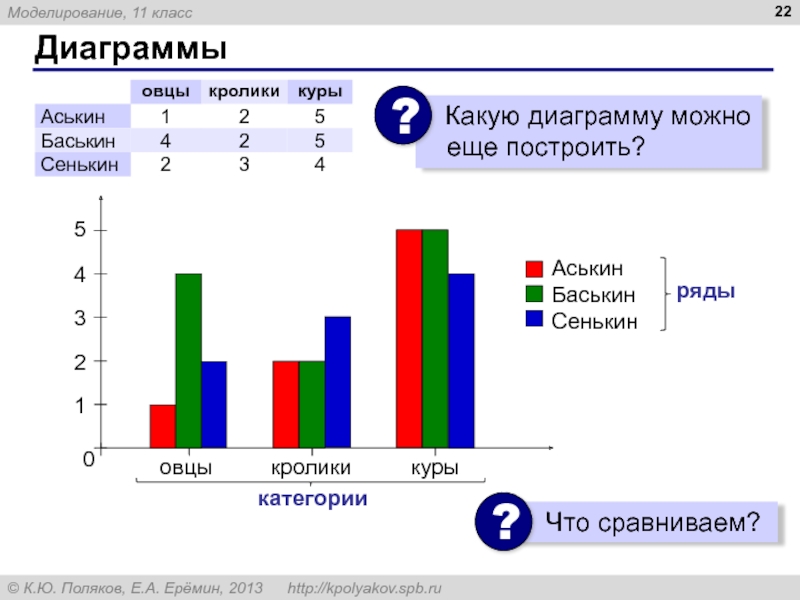
4. Какие типы диаграмм вы знаете? В каких случаях используется каждый из них?
*5. Изучите другие типы диаграмм, которые можно построить в табличных процессорах. Зачем они используются? Приведите примеры.
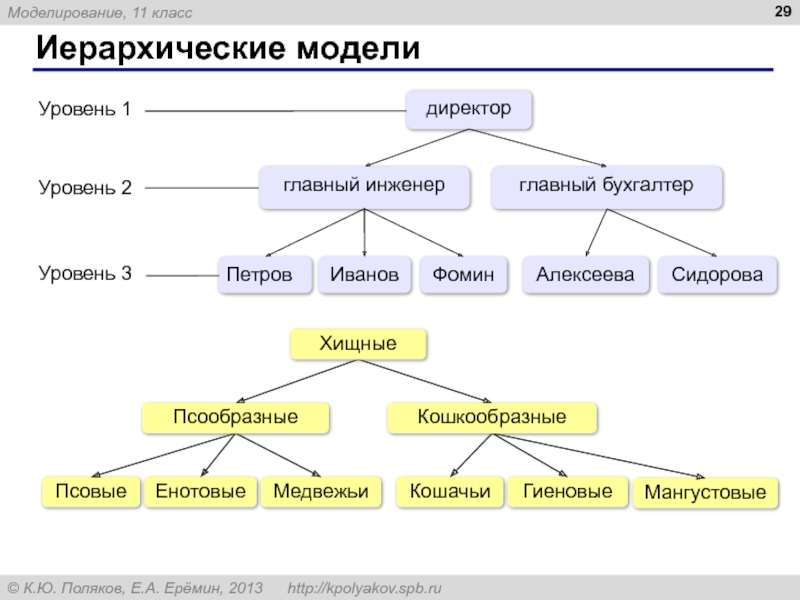
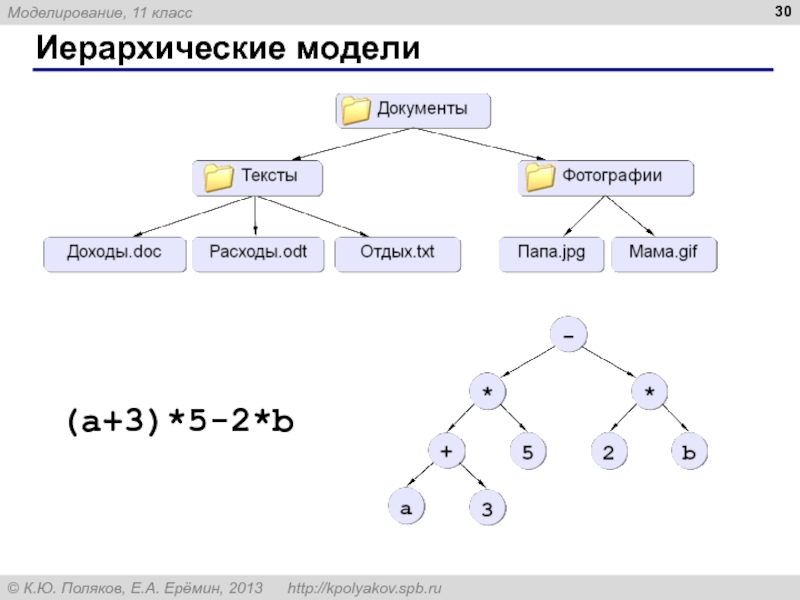
6. Объясните, почему любую систему, состоящую из подсистем, можно представить в виде иерархии.
7. Вспомните, что такое матрица смежности и весовая матрица графа (см. главу 1 в учебнике для 10 класса).
8. Зачем нужны сетевые модели при планировании производства?
9. Что такое семантические сети? В чем их достоинства и недостатки?
10. Что такое семантическая паутина? Можно ли её создать на основе существующих веб-страниц? Обоснуйте свой ответ.
11. Что такое выигрышная стратегия в игре?
12. Как доказать, что заданная позиция в игре является выигрышной (или проигрышной)? Как вы думаете, в каких случаях это сделать не удаётся?
13. Почему для того, чтобы доказать выигрыш какого-то игрока в заданной начальной позиции, не нужно строить полное дерево игры?

а) «Типы диаграмм»
б) «Сетевое планирование»
в) «Семантические сети»
г) «Интеллект-карты (mind maps)»
д) «Диаграммы Ганта»
е) «Использование ленты времени»

Задачи

1. В графе 9 узлов, причём каждый узел связан со всеми другими. Сколько всего связей в этой модели?

2. Система состоит из трёх подсистем по три элемента в каждой. Все элементы в каждой подсистеме связаны со всеми другими, кроме того, каждая подсистема связана со всеми другими подсистемами. Сколько всего связей в этой системе? Сравните ответы этой и предыдущей задач, сделайте выводы.

3. Постройте матрицы смежности и весовые матрицы для следующих графов.

4. Изготовление прибора «Заря-М» описывается следующей сетевой моделью (веса дуг обозначают длительность работ в днях).

Определите, через сколько дней после начала работ будет изготовлен прибор.

5. Постройте семантическую сеть на основе текста: «Кошачьи — семейство млекопитающих отряда хищных. Кроме кошек к ним относятся, например, львы и тигры. У кошачьих развиты слух и зрение. У нас дома живёт кошка Мурка. У неё рыжая шерсть».

6. Путешественник прибыл в посёлок Луковое в полночь по местному времени и увидел следующее расписание автобусов.

Определите самое раннее время, когда он может попасть в Васильево, и как ему нужно ехать.

7. Путешественник прибыл в посёлок Сычёво в 10:00 по местному времени и увидел следующее расписание автобусов.

Определите самое раннее время, когда он может попасть в посёлок Рогатое, и как ему нужно ехать.

8. Путешественник прибыл в посёлок Кунцево в полночь по местному времени и увидел следующее расписание автобусов.

Определите самое раннее время, когда он может попасть в посёлок Ручьи, и как ему нужно ехать.

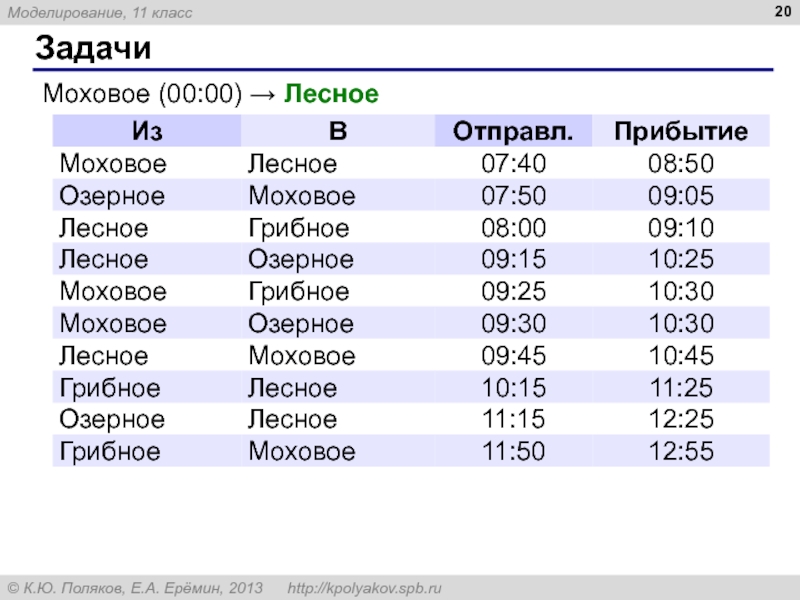
9. Путешественник прибыл в посёлок Моховое в полночь по местному времени и увидел следующее расписание автобусов.

Определите самое раннее время, когда он может попасть в посёлок Лесное, и как ему нужно ехать.

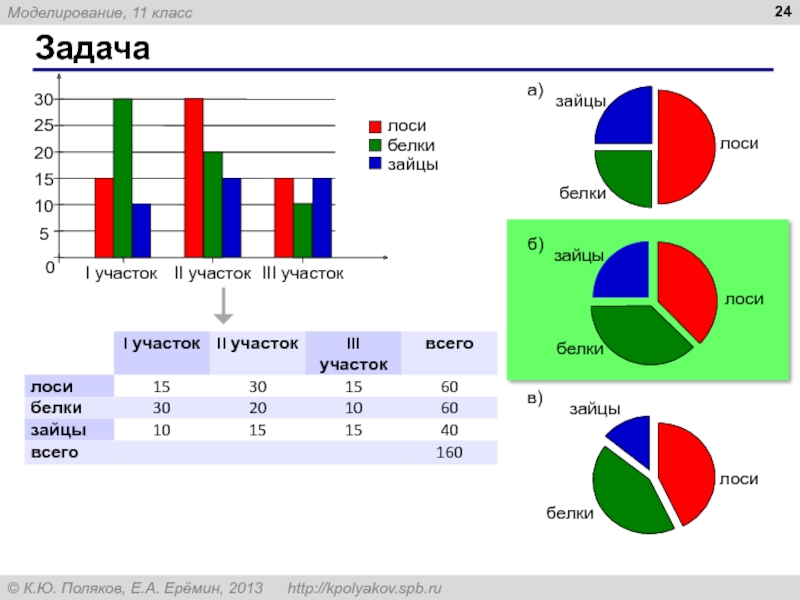
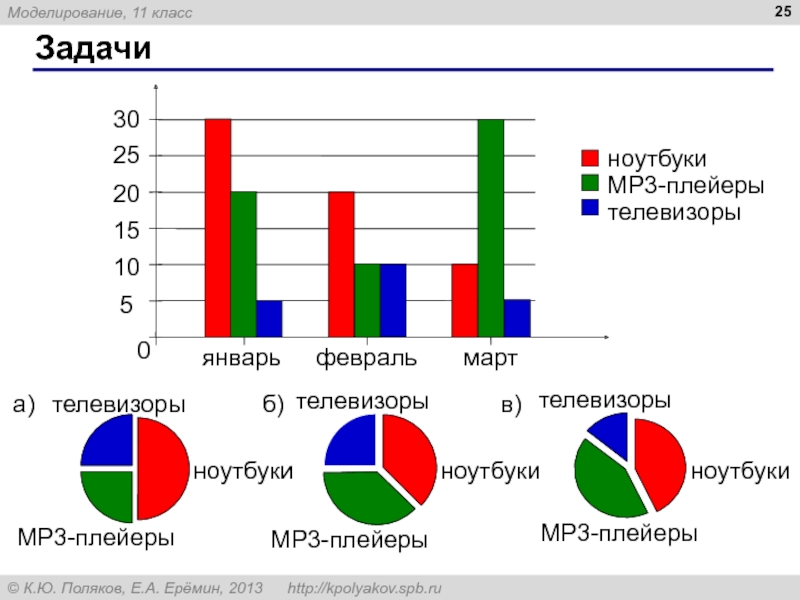
10. На диаграмме показано, сколько ноутбуков, МРЗ-плейеров и телевизоров продала некоторая фирма в первые три месяца года (I квартал).

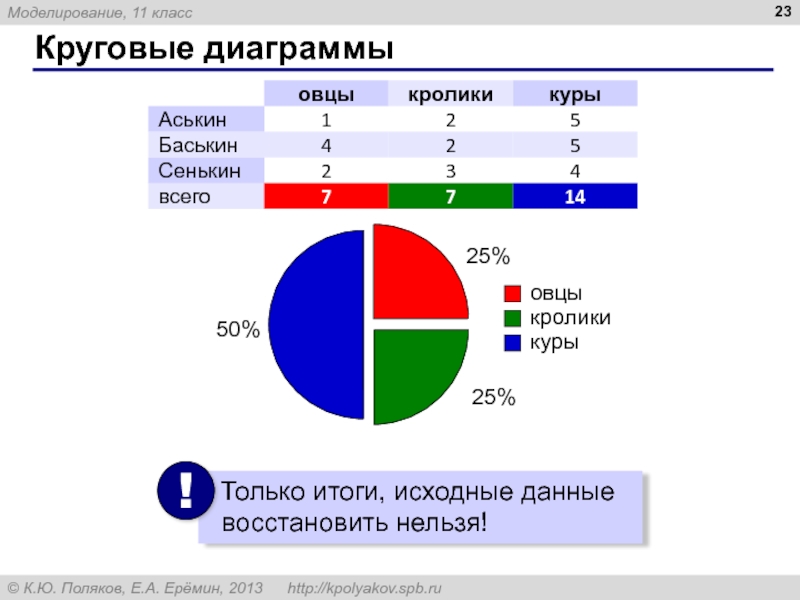
Какая из следующих диаграмм правильно отражает соотношение общего количества проданных товаров разных видов за весь I квартал?

11. В соревнованиях участвовали спортсмены из Москвы, Санкт- Петербурга и Мурманска, каждый из них имеет III, II или I разряд. На диаграмме 1) показано количество спортсменов, имеющих разные разряды, а на диаграмме 2) — соотношение спортсменов из разных городов.

Какие из этих утверждений следуют из анализа диаграмм:

а) все спортсмены, имеющие П разряд, могут быть москвичами;
б) все спортсмены из Мурманска могут иметь II разряд;
в) все спортсмены из Санкт-Петербурга могут иметь I разряд;
г) все спортсмены III разряда могут быть из Москвы?

12. В салоне продаются автомашины «Лада», «УАЗ» и «Ока» трёх цветов: красного, синего и зелёного. На диаграмме 1) показано количество машин разного цвета, а на диаграмме 2) — количество машин разных марок.

Какие из этих утверждений следуют из анализа диаграмм:

а) все автомобили «УАЗ» — зелёные;
б) среди автомобилей «Ока» нет красных;
в) все автомобили «Ока» — синие;
г) среди автомобилей «Лада» есть синие?

13. Два игрока играют в следующую игру. Вначале перед ними лежит куча из некоторого количества камней (обозначим его S). За один ход игрок может добавить в кучу 2 камня или увеличить количество камней в куче в два раза. У каждого игрока есть неограниченное количество камней. Победителем считается игрок, первым получивший кучу, в которой 25 камней или больше. Для каждого значения S (1 ? S ? 24) определите, кто выиграет и за сколько ходов. Для S = 7 постройте дерево игры, показывающее стратегию выигрывающего игрока.

14. Два игрока играют в следующую игру. Вначале перед ними лежит куча из некоторого количества камней (обозначим его S). За один ход игрок может добавить в кучу 1 камень или увеличить количество камней в куче в три раза. У каждого игрока есть неограниченное количество камней. Победителем считается игрок, первым получивший кучу, в которой 55 камней или больше. Для каждого значения S (1 ? S ? 54) определите, кто выиграет и за сколько ходов. Для S = 16 постройте дерево игры, показывающее стратегию выигрывающего игрока.

15. Два игрока играют в следующую игру. Вначале перед ними лежит куча из некоторого количества камней (обозначим его S). За один ход игрок может добавить в кучу два камня, добавить в кучу три камня или увеличить количество камней в куче в два раза. У каждого игрока есть неограниченное количество камней. Победителем считается игрок, первым получивший кучу, в которой 30 камней или больше. Для каждого значения S (1 ? S ? 29) определите, кто выиграет и за сколько ходов. Для S = 9 постройте дерево игры, показывающее стратегию выигрывающего игрока.

16. Игра Баше. Два игрока играют в следующую игру. Вначале перед ними лежит куча из некоторого количества камней (обозначим его S). За один ход игрок может взять из кучи 1, 2 или 3 камня. Выигрывает тот, кто возьмет последний камень. Для каждого значения S (1 ? S ? 15) определите, кто выиграет и за сколько ходов. Для S = 12 постройте дерево игры, показывающее стратегию выигрывающего игрока.

Источник

Презентация на тему Модели и моделирование. Системный подход в моделировании. Этапы моделирования. Математические модели в биологии

Презентация на тему Презентация на тему Модели и моделирование. Системный подход в моделировании. Этапы моделирования. Математические модели в биологии, предмет презентации: Информатика. Этот материал содержит 76 слайдов. Красочные слайды и илюстрации помогут Вам заинтересовать свою аудиторию. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций ThePresentation.ru в закладки!

Слайды и текст этой презентации

§ 6. Модели и моделирование
§ 7. Системный подход в моделировании
§ 8. Этапы моделирования
§ 9. Моделирование движения
§ 10. Математические модели в биологии
§ 11. Системы массового обслуживания

объекты (самолет, дом, ядро атома, галактика)
процессы (изменение климата, развитие экономики)
явления природы (землетрясения, цунами)

оригинал не существует
древний Египет
последствия ядерной войны (Н.Н. Моисеев, 1966)
исследование оригинала дорого или опасно
управление ядерным реактором (Чернобыль, 1986)
испытание нового скафандра для космонавтов
разработка нового самолета или корабля
оригинал сложно исследовать
Солнечная система, галактика (большие размеры)
атом, нейтрон (маленькие размеры)
процессы в двигателе внутреннего сгорания (очень быстрые)
геологические явления (очень медленные)
интересуют только отдельные свойства
проверка краски для фюзеляжа самолета

Нужно решить задачу, связанную с оригиналом, но:

Модель – это объект, который обладает существенными свойствами другого объекта, процесса или явления (оригинала) и используется вместо него.

Моделирование – это создание и исследование моделей с целью изучения оригиналов.

Задачи моделирования:
исследование оригинала
анализ («что будет, если …»)
синтез («как сделать, чтобы …»)
оптимизация («как сделать лучше всего …»)

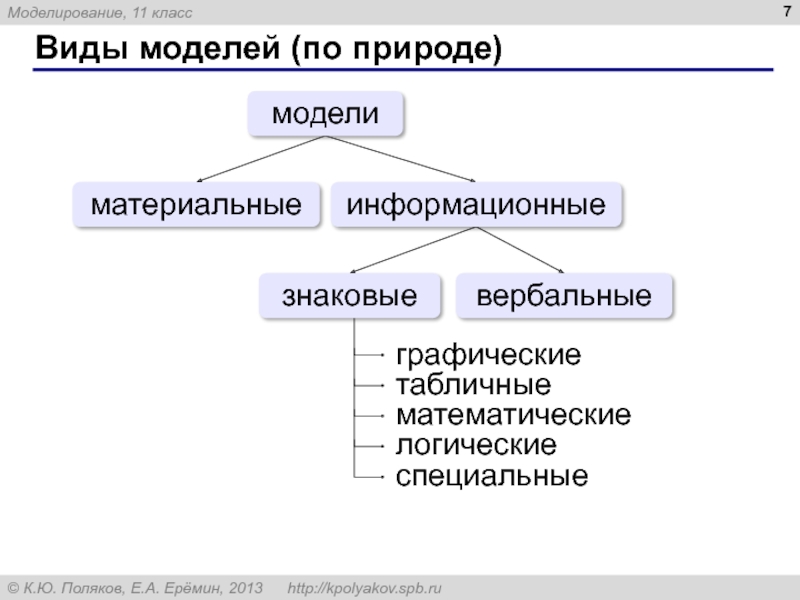
Виды моделей (по фактору времени)

статические – описывают оригинал в заданный момент времени
силы, действующие на тело в состоянии покоя
результаты осмотра врача
фотография
…
динамические
модель движения тела
явления природы (молния, землетрясение, цунами)
история болезни
видеозапись события
…

Виды моделей (по характеру связей)

детерминированные – при одинаковых исходных данных всегда получается тот же результат
расчёт по формулам
движение корабля на спокойной воде
…
вероятностные – учитывают случайность событий
броуновское движение частиц
полета самолёта с учетом ветра
движения корабля на волнении
поведение человека
…

нельзя заранее вычислить или предсказать поведение системы, но можно имитировать её реакцию на внешние воздействия
максимальный учет всех факторов
только численные результаты

Примеры:
испытания лекарств на мышах, обезьянах, …
математическое моделирование биологических систем
модели систем массового обслуживания
модели процесса обучения
кросс-программирование
…

экономические ситуации
военные действия
спортивные игры
тренинги персонала

Игровые модели учитывают действия противников.

Адекватность – это совпадение существенных свойств модели и оригинала в данной задаче.

Модель всегда отличается от оригинала

результаты моделирования согласуются с выводами теории (законы сохранения и т.п.)
… подтверждаются экспериментом (±10%)

§ 7. Системный подход в моделировании

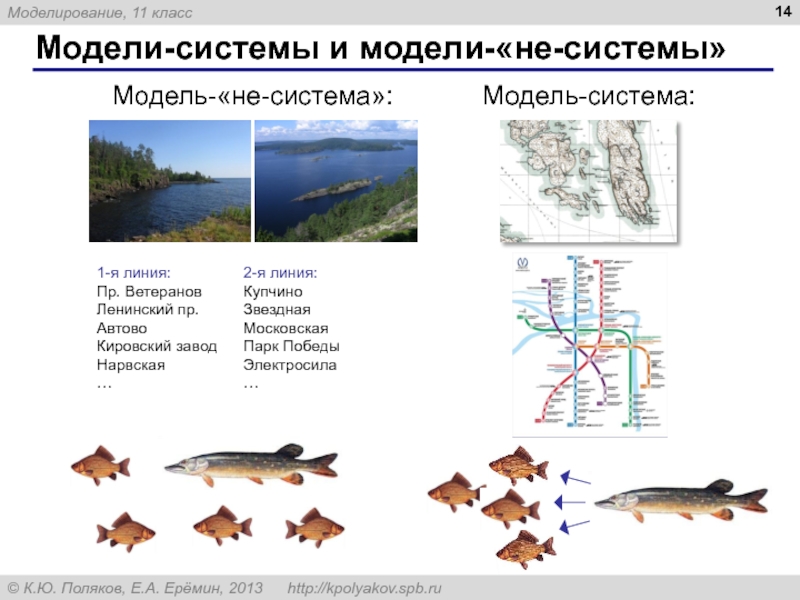
Модели-системы и модели-«не-системы»

1-я линия:
Пр. Ветеранов
Ленинский пр.
Автово
Кировский завод
Нарвская
…

2-я линия:
Купчино
Звездная
Московская
Парк Победы
Электросила
…

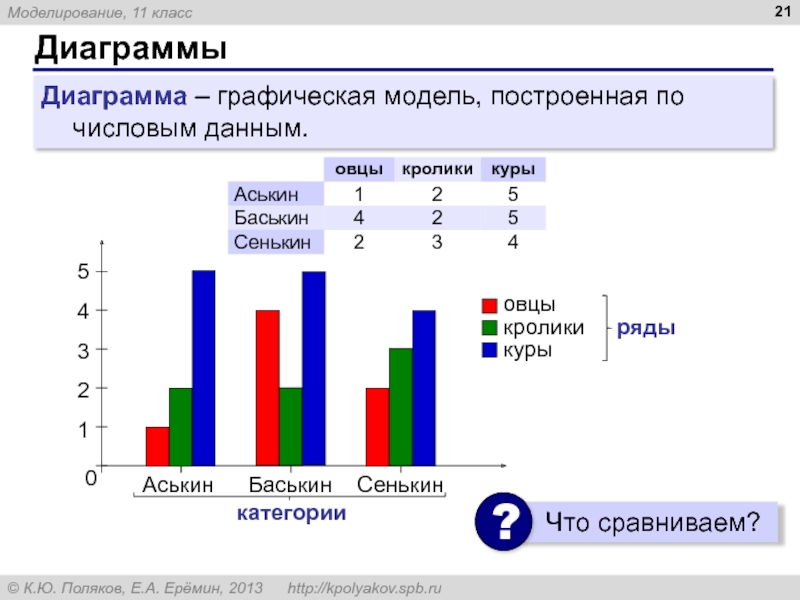
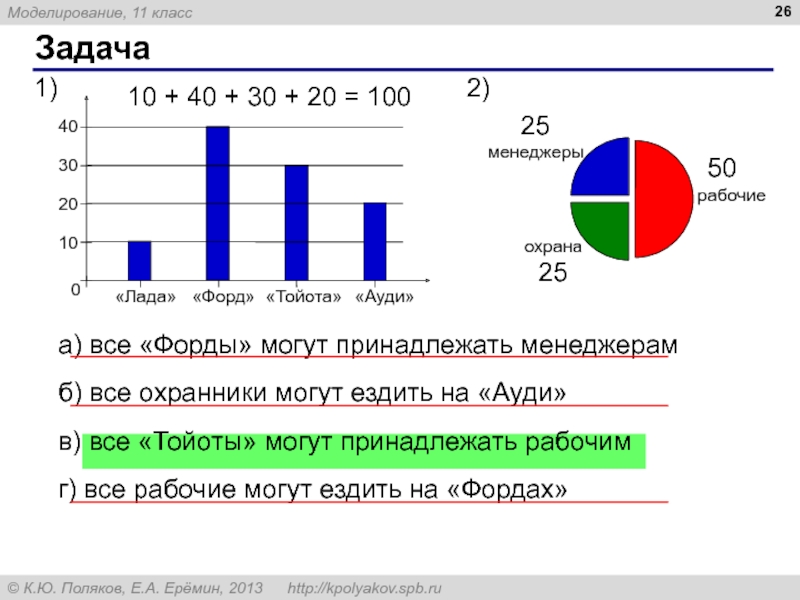
Диаграмма – графическая модель, построенная по числовым данным.

а) все «Форды» могут принадлежать менеджерам
б) все охранники могут ездить на «Ауди»
в) все «Тойоты» могут принадлежать рабочим
г) все рабочие могут ездить на «Фордах»

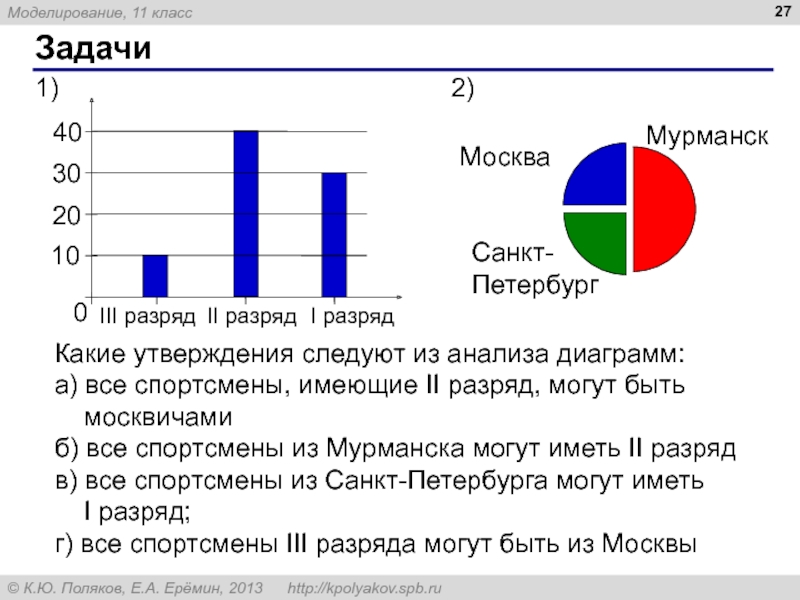
Какие утверждения следуют из анализа диаграмм:
а) все спортсмены, имеющие II разряд, могут быть москвичами
б) все спортсмены из Мурманска могут иметь II разряд
в) все спортсмены из Санкт-Петербурга могут иметь I разряд;
г) все спортсмены III разряда могут быть из Москвы

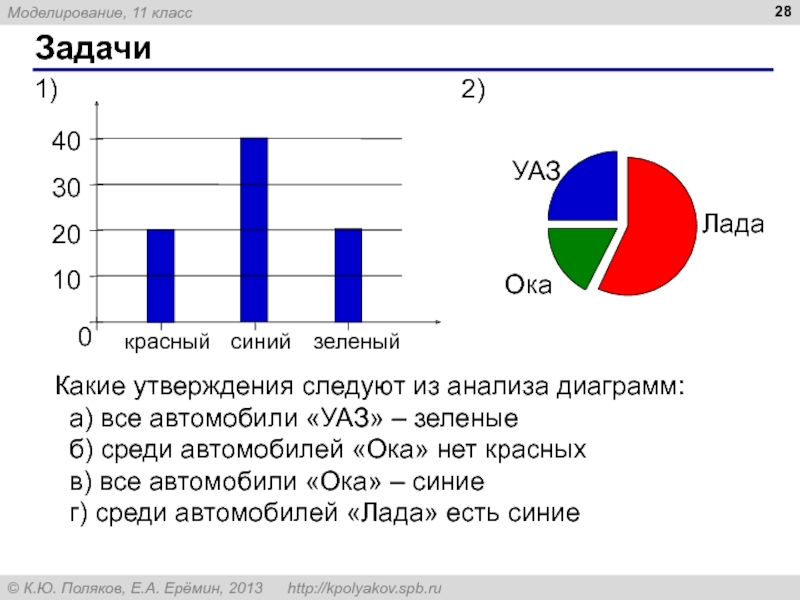
Какие утверждения следуют из анализа диаграмм:
а) все автомобили «УАЗ» – зеленые
б) среди автомобилей «Ока» нет красных
в) все автомобили «Ока» – синие
г) среди автомобилей «Лада» есть синие

Построить матрицы смежности и весовые матрицы.

Задача: определить срок изготовления прибора.

Задача: найти стратегию (алгоритм игры), который позволит получить лучший результат, если соперники играют безошибочно.

Игры с полной информацией: можно определить, кто должен выиграть, по начальной позиции.

Позиции:
проигрышные – все возможные ходы ведут в выигрышные позиции
выигрышные – хотя бы один ход ведёт в проигрышную позицию

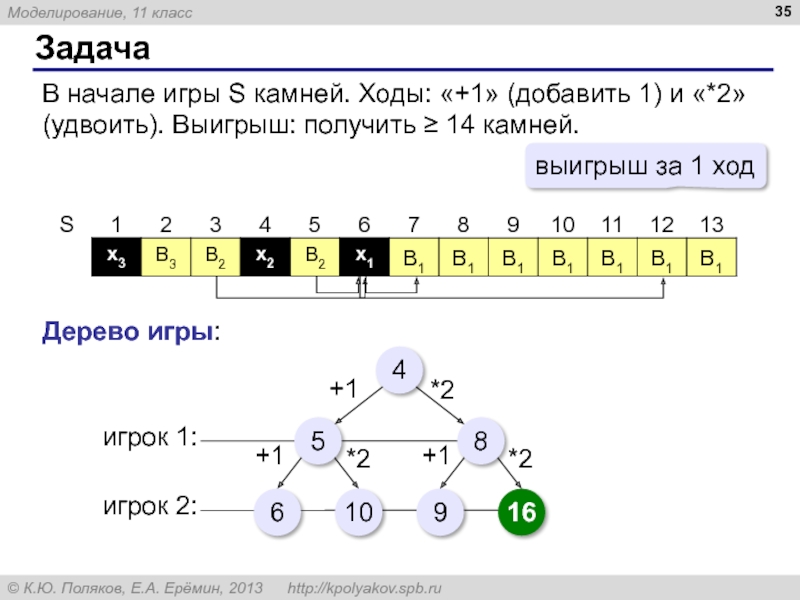
В начале игры S камней. Ходы: «+1» (добавить 1) и «*2» (удвоить). Выигрыш: получить ≥ 14 камней.

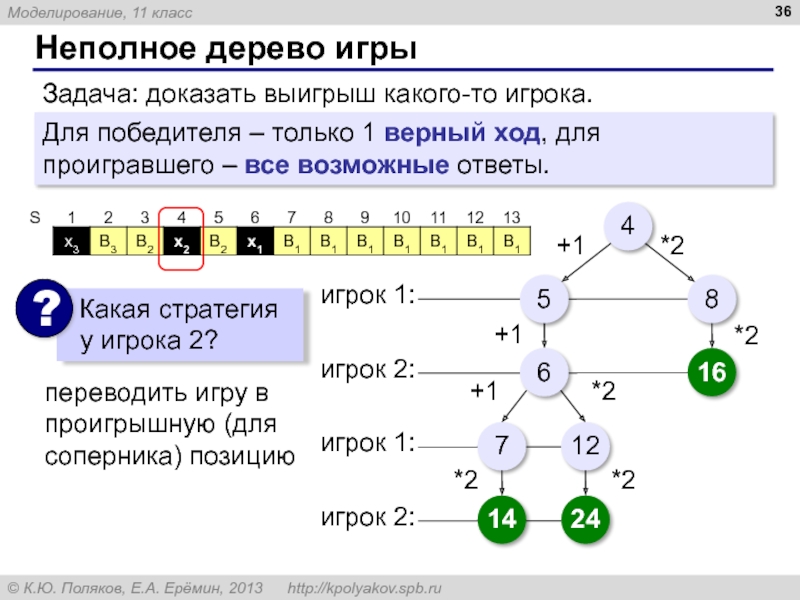
Задача: доказать выигрыш какого-то игрока.

Для победителя – только 1 верный ход, для проигравшего – все возможные ответы.

переводить игру в проигрышную (для соперника) позицию

В начале игры S камней. Ходы: «+2» (добавить 2) и «*2» (удвоить). Выигрыш: получить ≥ 25 камней. Построить дерево игры для S = 7.
В начале игры S камней. Ходы: «+1» (добавить 1) и «*3» (утроить). Выигрыш: получить ≥ 55 камней. Построить дерево игры для S = 16.
В начале игры S камней. Ходы: «+2» (добавить 2), «+3» (добавить 3) и «*2» (удвоить). Выигрыш: получить ≥ 30 камней. Построить дерево игры для S = 9.
Игра Баше. В начале игры S (S ≤ 15) камней. Ходы: «-1» (взять 2), «-2» (взять 2) и «-3» (взять 3). Проигрыш: взять последний камень. Построить дерево игры для S = 12.

исследование оригинала
изучение сущности объекта или явления
анализ («что будет, если …»)
научиться прогнозировать последствий при различных воздействиях на оригинал
синтез («как сделать, чтобы …»)
научиться управлять оригиналом, оказывая на него воздействия
оптимизация («как сделать лучше»)
выбор наилучшего решения в заданных условиях

Хорошо поставленная задача:
описаны все связи между исходными данными и результатом
известны все исходные данные
решение существует
задача имеет единственное решение
Примеры плохо поставленных задач:
Уроки в школе начинаются в 830. В 1000 к школе подъехал красный автомобиль. Определите, когда Вася выйдет играть в футбол?
Вася бросает мяч со скоростью 12 м/с. Где мяч впервые ударится о землю?
Решить уравнение sin x = 4 (нет решений).
Найти функцию, которая проходит через точки (0,1) и (1,0) (бесконечно много решений).

I. Постановка задачи (пример)

Спортсмен Вася в синей кепке бросает белый мяч со скоростью 12 м/с. Под каким углом к горизонту ему нужно бросить мяч, чтобы попасть в желтую мишень?

Спортсмен Вася в синей кепке бросает белый мяч со скоростью 12 м/с. Под каким углом к горизонту ему нужно бросить мяч, чтобы попасть в желтую мишень? Мишень расположена на высоте 4 м на расстоянии 10 м от Васи. В момент броска мяч находится на высоте 2 м от земли.

1) Определить существенные исходные данные.

мяч и мишень — материальные точки
мишень неподвижна
сопротивление воздуха не учитывается.

Источник